残差勾配 \(\mathrm{E}[\varepsilon(n) x(n - m)]\) の挙動観察/Signed-LMSの目的関数の2階微分

残差勾配 \(\mathrm{E}[\varepsilon(n) x(n - m)]\) の挙動観察

\(m\) が大きいときは無視できるのでは？ なお、長時間平均値は0に収束していることを見た。 \(m\) をずらした時の平均値の様子を見る。どこかで影響が小さくなって打ち切れるはず。

  • ガチャガチャ弄ってるってるけど示唆があんまりない。
  • 低次（〜10）の係数は大きく変動する傾向。しかし、次に述べるピッチなどに影響しているのか、全てに当てはまる傾向ではない。
  • \(\mathrm{E}[\varepsilon(n) x(n - m)]\) は \(m\) を大きくすれば単調減少するわけではない。音源依存で傾向が異なる。ピッチ？か何かに反応して大きくなる場合がある。
  • 同一発音区間では、フィルタ係数の符号は同一になる傾向が見られる。単一のsin波を等価させたときはわかりやすい。
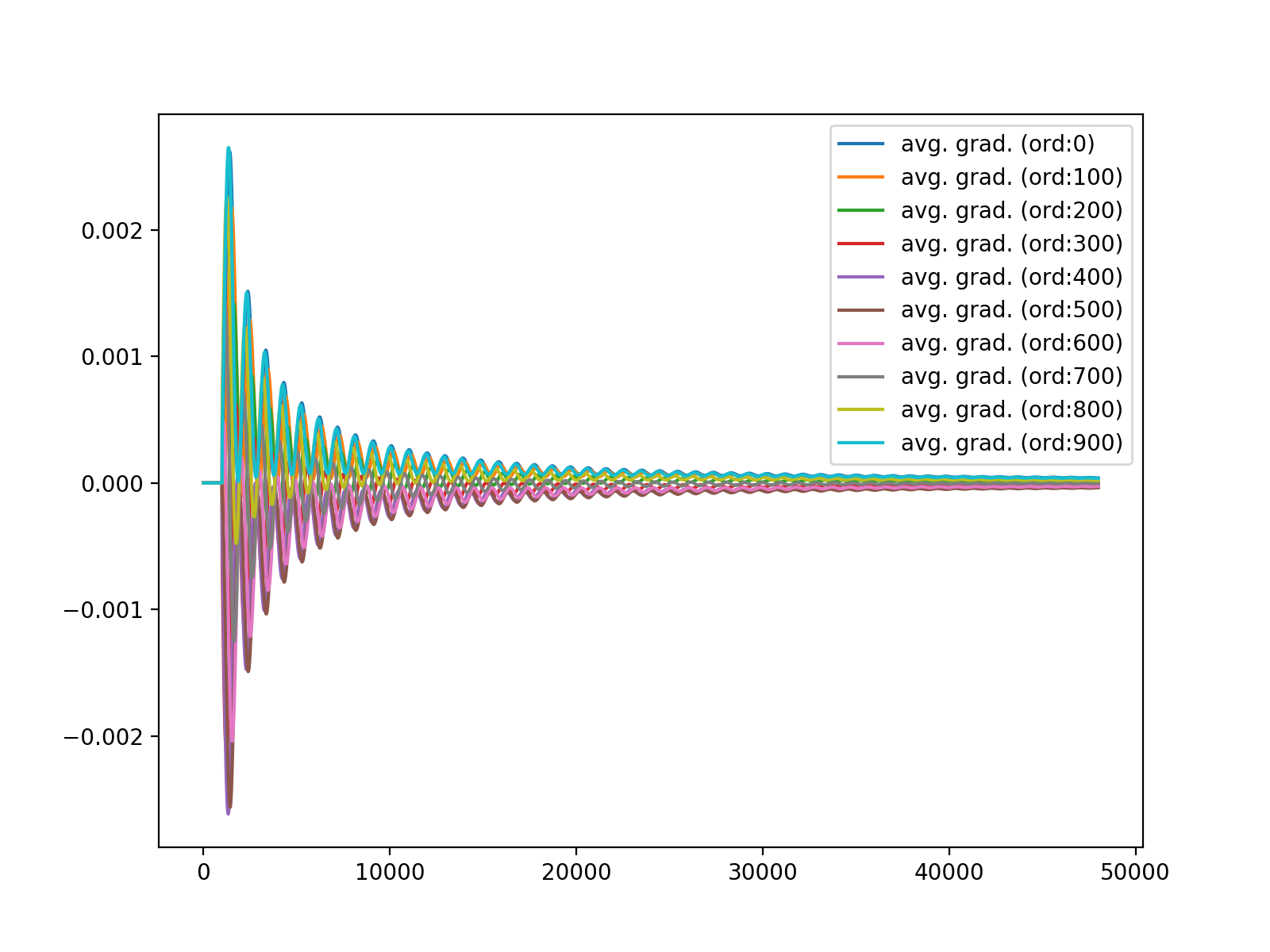
440.0Hzのsin波に対する各タップの平均勾配変化グラフ

440.0Hzのsin波に対する各タップの平均勾配変化

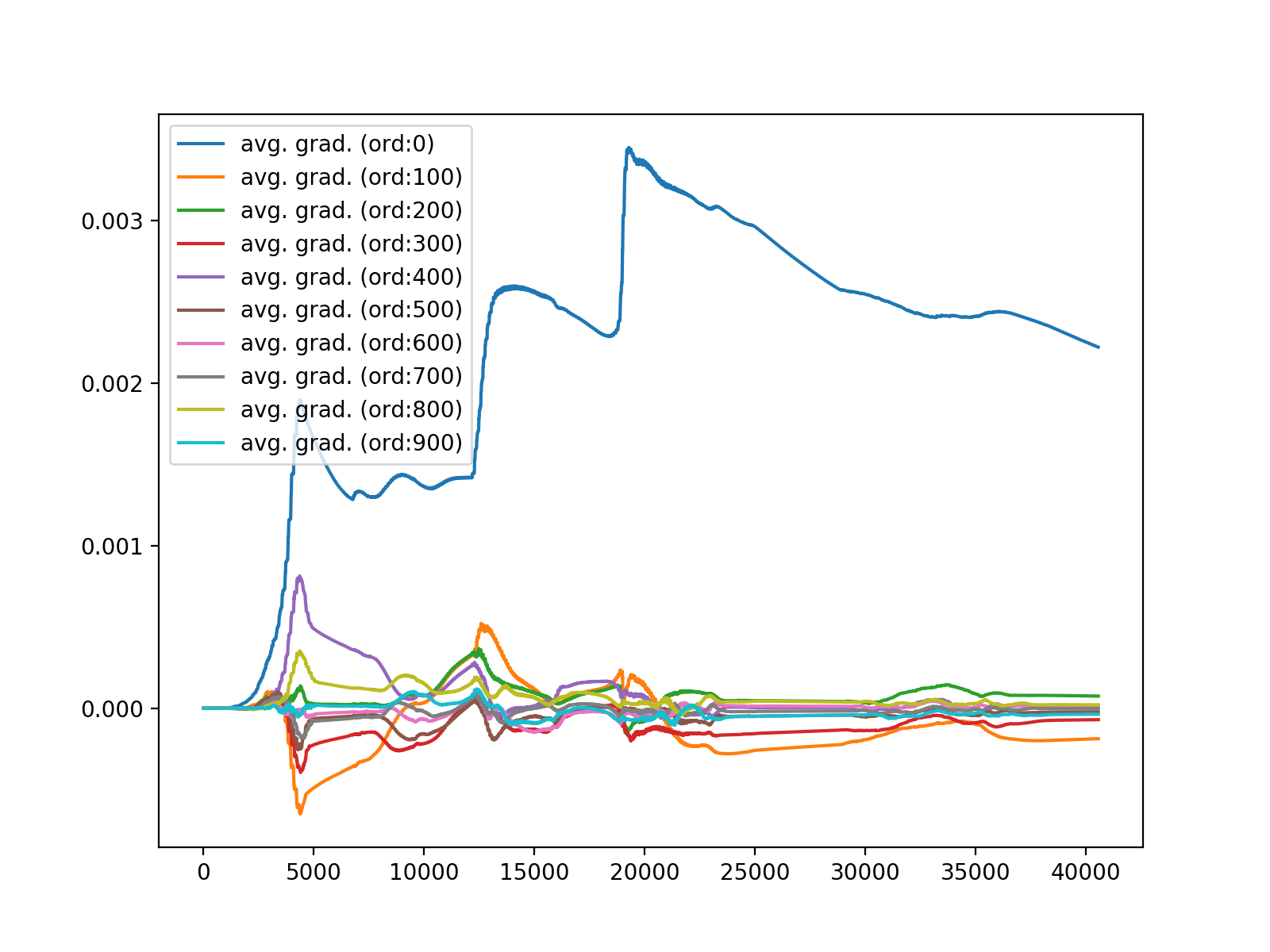
ボイス対する各タップの平均勾配変化グラフ

ボイス対する各タップの平均勾配変化

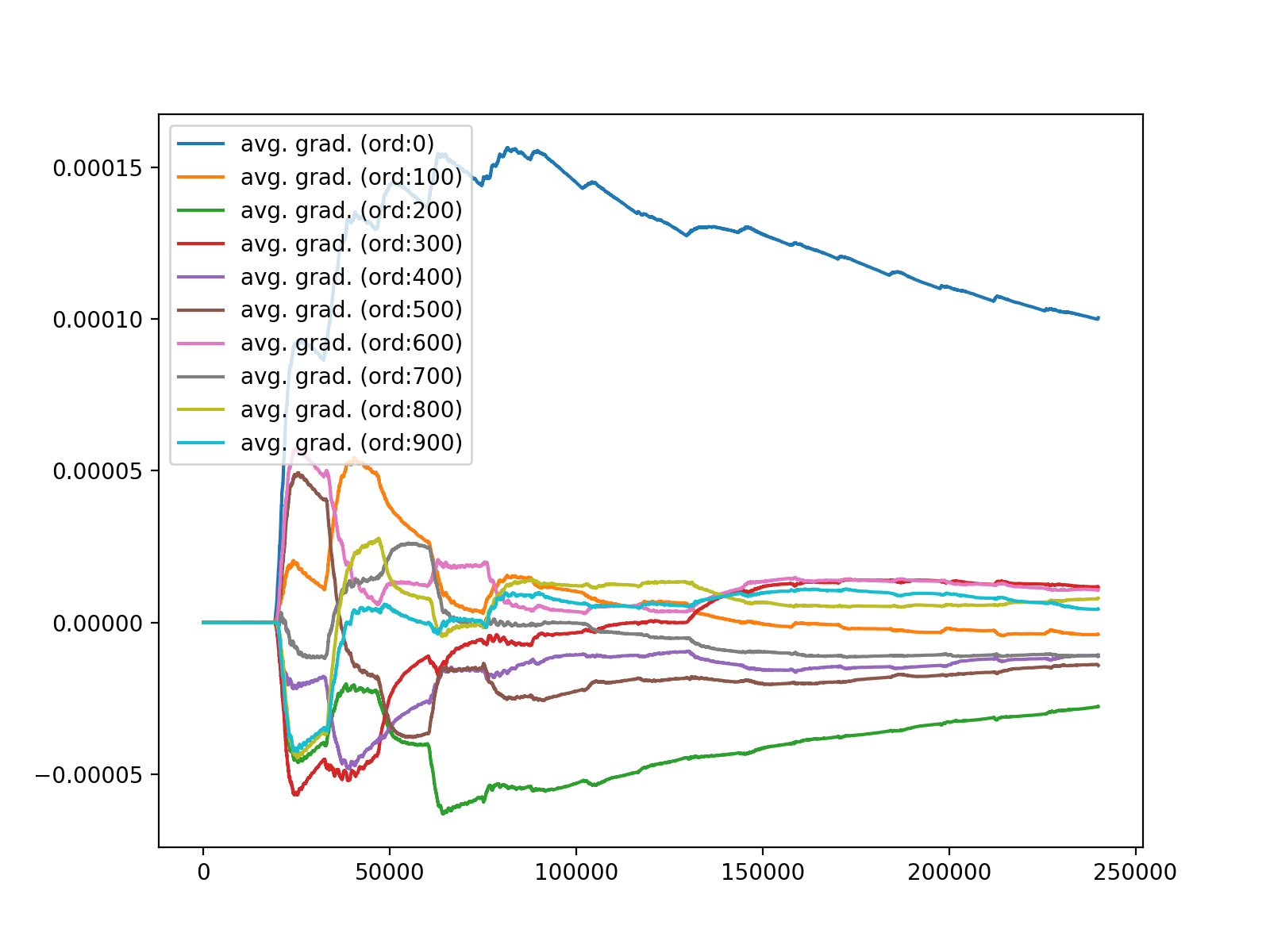
ピアノ演奏に対する各タップの平均勾配変化グラフ

ピアノ演奏に対する各タップの平均勾配変化

Signed-LMSの目的関数の2階微分

勇気を出してやってみる。

\begin{equation*} \newcommand\innerp[2]{\langle #1, #2 \rangle} \newcommand\ve[1]{\boldsymbol{#1}} \newcommand\parfrac[2]{\frac{\partial #1}{\partial #2}} \end{equation*}

符号関数を \(\tanh(Tx)\) で近似して微分してみる（\(T\) は温度パラメータで、\(\tanh(Tx)\) を \(T \to \infty\) ならしめれば符号関数に近づく）と、

\begin{equation*} \frac{d}{dx} \tanh(Tx) = T (\tanh(Tx))^{\prime} = T(1 - \tanh^{2}(Tx)) \end{equation*}

さて、 \(1 - \tanh^{2}(Tx)\) に注目すると、\(T\) の極限では \(x = 0\) を除き0を取るが、\(x = 0\) において1を取る。よってこれはインパルス関数になる（極限と微分操作を交換したけどやかましいことは暗黙で...）。

符号関数を微分するとインパルス関数が出てくることについては 超関数的微分_δ関数関連（２） を見るのが早いかも。以下では、その話に従って、\(\frac{d}{dx} \mathrm{sign}(x) = 2\delta(x)\) とする。

さて、今一度評価関数 \(\mathrm{E}[|\varepsilon(n)|]\) の偏微分と2階の偏導関数を考える。

\begin{align*} \parfrac{}{h(m)} \mathrm{E}[|\varepsilon(n)|] &= \mathrm{E}\left[ \parfrac{}{h(m)} |\varepsilon(n)| \right] \\ &= \mathrm{E}\left[ \left\{ \parfrac{}{h(m)} \varepsilon(n) \right\} \mathrm{sign}[\varepsilon(n)] \right] \\ &= -\mathrm{E}\left[ \mathrm{sign}[\varepsilon(n)] x(n - m) \right] \\ \frac{\partial^{2}}{\partial h(m) \partial h(k)} \mathrm{E}[|\varepsilon(n)|] &= - \parfrac{}{h(k)} \mathrm{E}\left[ \mathrm{sign}[\varepsilon(n)] x(n - m) \right] \\ &= - \mathrm{E}\left[ \left\{ \parfrac{}{h(k)} \varepsilon(n) \right\} 2\delta(\varepsilon(n)) x(n - m) \right] \\ &= 2\mathrm{E}\left[ \delta(\varepsilon(n)) x(n - m) x(n - k) \right] \end{align*}

ここで \(\mathrm{E}\left[ \delta(\varepsilon(n)) x(n - m) x(n - k) \right]\) に注目する。これは \(\varepsilon(n) = 0\) のときだけ和を取る演算だ。\(\sum\) を用いると、

\begin{equation*} \mathrm{E}\left[ \delta(\varepsilon(n)) x(n - m) x(n - k) \right] = \lim_{N \to \infty} \frac{1}{N} \sum_{n = 1, \varepsilon(n) = 0}^{N} x(n - m) x(n - k) \end{equation*}

という計算に該当する。厳密計算は \(\varepsilon(n) = 0\) なる \(n\) を見つけたら足していく感じでいいと思うけど、今は \(\varepsilon(n)\) はラプラス分布に従うと仮定している。だからラプラス分布に従って \(P(\varepsilon(n) = 0) = \frac{1}{2\lambda}\) （分散 \(2\lambda^{2}\) ）の重み付けをして計算してしまって良いように見えるのだがどうなんだろう。なんか怪しくて考え続けている。

もし適応フィルタに組み込むなら、残差が0になったら上の式に従ってヘッセ行列を更新し、ニュートン法を使い続ける。これは試してみたい。問題はヘッセ行列が逆行列を持つかというところ…4-20で半正定値であることは確認したが正定値とは限らない。共役勾配法を検討する必要があるかも。\(\ve{X}\ve{X}^{\mathsf{T}}\) は正則になるとは思えない…。（軽く試したけどすぐにだめな例が見つかった。）

他の頂いたアイディア

  • 周波数領域に一旦飛ばすのはあり？
    • ありだけど計算量が高い。圧縮率が上がるのであれば大アリ。
  • 確率的PCAとか使えない？辞書は小さくて済む。
  • 線形ダイナミクスにより上手く定式化できない？

優先度低