フーリエ変換について
フーリエ変換が天下りに与えられて次の言明に対して違和感を抱いたことは無いだろうか?
任意の周期関数は三角関数の和で表現できる
といった手合いである。この言明に対しては、次の疑問が浮かぶかもしれない:
- 任意の周期関数に対して成り立つのか?
- 何故三角関数を用いる必要があるのか?三角関数である必然性は?
本稿では、この疑問に対して数学的に一応の解答を与えたい。細かい解説は後にして、解答としては次の様になる。
- 任意の区分的になめらかな周期関数は三角関数の和で表現できる
- 三角関数は連続関数を表現できる能力を持っている
以下、これらの項目の証明を試みる。
関数はベクトル
形式的に見れば、 関数はベクトル である。関数は入力と出力を決める規則であることから、 式1 の様に、その出力を並べることで、関数をベクトルとして見ることが出来る。
\begin{align*}
f(x) = \vvec{ f(-\infty) \\ \vdots \\ f(0) \\ \vdots \\ f(\infty) } \tag{1}
\end{align*}
関数をベクトルとみなすと、そこに線型代数の知見を持ち込むことができる。まず、関数による基底(関数基底)によって空間を張ることができる。関数によって張られた空間は特に 関数空間 と呼ばれる。
また、2つの関数 \(f,g\) の 内積 \(\innerp{f}{g}\) を式 式2 の様に積分を用いて表すことが出来る。
\begin{align*}
\innerp{f}{g} &=
\left[ f(-L) \dots f(0) \dots f(L) \right]
\vvec{ g(-L) \\ \vdots \\ g(0) \\ \vdots \\ g(L) } \\
&= f(-L)g(-L) + \dots + f(0)g(0) + \dots + f(L)g(L) \\
&= \int_{-L}^{L} f(x)g(x) dx \tag{2}
\end{align*}
ここで \(L\) は積分範囲を決める定数である 。また、関数自分自身の内積 \(\innerp{f}{f}\) を ノルム という 。
三角関数の直交性
関数をベクトルとして考えた時、異なる周波数を持つ三角関数は互いに直交(\(\iff\) 内積値が \(0\) になる)する。この事を計算により確かめていく。
尚、内積計算時の積分範囲は全て \([-\pi, \pi]\) とする。何故なら、周期関数が直交しているかどうかを判定するには1周期分の内積を取り、その結果が \(0\) になるかどうかを見れば良いからである。またその周期は、周波数を決める定数は全て整数であることにより決まり、最長の周波数は \(\sin(x), \cos(x)\) が持つ \(2\pi\) である。積分範囲を \([-\pi, \pi]\) とすれば、一番長い周期を加味して内積を計算できる。
正弦波(sin)の直交性
素直に内積を計算する。三角関数の和の公式
\begin{align*}
\cos\{(n+m)x\} &= \cos(nx)\cos(mx) - \sin(nx)\sin(mx) \\
\cos\{(n-m)x\} &= \cos(nx)\cos(mx) + \sin(nx)\sin(mx) \\
\implies \sin(nx)\sin(mx) &= \frac{\cos\{(n-m)x\} - \cos\{(n+m)x\}}{2}
\end{align*}
を用いて \(\sin\) の積を \(\cos\) の和に分割して積分を行うのがポイントである。
\begin{align*}
\innerp{\sin(nx)}{\sin(mx)}
&= \int_{-\pi}^{\pi} \sin(nx) \sin(mx) dx \\
&= \int_{-\pi}^{\pi} \frac{\cos\{(n-m)x\} - \cos\{(n+m)x\}}{2} dx \\
&= \frac{1}{2(n-m)} \left[ \sin\{(n-m)x\} \right]_{-\pi}^{\pi} - \frac{1}{2(n+m)} \left[ \sin\{(n+m)x\} \right]_{-\pi}^{\pi} \\
&= \frac{1}{2(n-m)} \left[ \sin\{(n-m)\pi\} - \sin\{-(n-m)\pi\} \right] - \frac{1}{2(n+m)} \left[ \sin\{(n+m)\pi\} - \sin\{-(n+m)\pi\} \right] \\
&= \frac{\sin\{(n-m)\pi\}}{n-m} - \frac{\sin\{(n+m)\pi\}}{n+m}
\end{align*}
ここで、最後の結果の右辺第二項は、\(n+m\) が整数になることから \(0\) になる。一方の右辺第一項は \(n \neq m\) の時は右辺第二項と同様に \(0\) となる。 \(n = m\) の時は、 \(n-m \to 0\) なる極限を考えることで計算結果が確かめられる:
\begin{align*}
\lim_{(n-m) \to 0} \frac{\sin\{(n-m)\pi\}}{n-m}
&= \lim_{\alpha \to 0} \frac{\sin\alpha\pi}{\alpha} \\
&= \lim_{\alpha \to 0} \frac{\ddiff{\sin\alpha\pi}{\alpha}}{\ddiff{\alpha}{\alpha}} = \lim_{\alpha \to 0} \pi \cos\alpha\pi \\
&= \pi \tag{3}
\end{align*}
以上の結果をまとめると、
\begin{align*}
\innerp{\sin(nx)}{\sin(mx)} = \ifdiv{cc}{ 0 & (n \neq m) \\ \pi & (n = m) } \tag{4}
\end{align*}
この結果は、2つの意味で重要である。
- (今確かめている様に、)異なる周波数を持つ正弦波は互いに直交する。
- \(n=m\) の時の結果は、 \(\sin\) のノルム値は \(\pi\) であることを示している。
余弦波(cos)の直交性
計算方針は \(\sin\) の時と同様である。三角関数の和の公式より、
\begin{equation*}
\cos(mx)\cos(nx) = \frac{\cos\{(n-m)x\} + \cos\{(n+m)x\}}{2}
\end{equation*}
が成立するため、
\begin{align*}
\innerp{\cos(nx)}{\cos(mx)}
&= \int_{-\pi}^{\pi} \cos(nx) \cos(mx) dx \\
&= \int_{-\pi}^{\pi} \frac{\cos\{(n-m)x\} + \cos\{(n+m)x\}}{2} dx \\
&= \frac{1}{2(n-m)} \left[ \sin\{(n-m)\pi\} - \sin\{-(n-m)\pi\} \right] + \frac{1}{2(n+m)} \left[ \sin\{(n+m)\pi\} - \sin\{-(n+m)\pi\} \right] \\
&= \frac{\sin\{(n-m)\pi\}}{n-m} + \frac{\sin\{(n+m)\pi\}}{n+m}
\end{align*}
と、\(\sin\) の内積計算時とほぼ同様の結果が得られる。最終結果の第一項に関しては式 式3 と同様に考えることで、次の結果が得られる。
\begin{align*}
\innerp{\cos(nx)}{\cos(mx)} = \ifdiv{cc}{ 0 & (n \neq m) \\ \pi & (n = m) } \tag{5}
\end{align*}
\(\cos\) のノルムも \(\sin\) と同様 \(\pi\) であることが示されている。
正弦波と余弦波の直交性
最後に \(\sin\) と \(\cos\) の直交性を確かめる。
三角関数の和の公式により、
\begin{align*}
\sin\{(n+m)x\} &= \sin(nx)\cos(mx) + \cos(nx)\sin(mx) \\
\sin\{(n-m)x\} &= \sin(nx)\cos(mx) - \cos(nx)\sin(mx) \\
\implies \sin(nx)\cos(mx) &= \frac{\sin\{(n+m)x\} + \sin\{(n-m)x\}}{2}
\end{align*}
が成立するため、
\begin{align*}
\innerp{\sin(mx)}{\cos(mx)}
&= \int_{-\pi}^{\pi} \sin(nx) \cos(mx) dx \\
&= \int_{-\pi}^{\pi} \frac{\sin\{(n+m)x\} + \sin\{(n-m)x\}}{2} dx \\
&= \frac{1}{2(n+m)} \left[ \cos\{(n+m)\pi\} - \cos\{-(n+m)\pi\} \right] + \frac{1}{2(n-m)} \left[ \cos\{(n-m)\pi\} - \cos\{-(n-m)\pi\} \right] \\
&= 0
\end{align*}
従って、如何なる周波数に対しても正弦波と余弦波は直交していること
\begin{equation*}
\innerp{\sin(nx)}{\cos(mx)} = 0 \tag{6}
\end{equation*}
が確かめられた。
フーリエ係数
次の様に信号 \(f(x)\) がフーリエ級数展開されていたとする。
\begin{equation*}
f(x) = \frac{1}{2} a_{0} + \sum_{k=1}^{\infty} a_{k} \cos(kx) + \sum_{k=1}^{\infty} b_{k} \sin(kx)
\end{equation*}
上式における係数 \(a_{0}, a_{1}, ..., b_{1}, b_{2}, ...\) はフーリエ級数と呼ばれる。
フーリエ係数は、周波数成分への重み付けと説明される事が多い。一方、上記のように関数をベクトルとみなすと、信号を三角関数基底で表した際の一次結合係数とも捉え直す事ができる。
係数を取り出すには、上記の直交性( 式4, 式5, 式6 )を使用すれば良い。\(\innerp{f(x)}{\sin(nx)} \ n \in \mathbb{N}\) を計算すると、
\begin{align*}
\innerp{f(x)}{\sin(nx)}
&= \innerp{\frac{1}{2} a_{0} + \sum_{k=1}^{\infty} a_{k} \cos(kx) + \sum_{k=1}^{\infty} b_{k}\sin(kx)}{\sin(nx)} \\
&= \innerp{\frac{1}{2} a_{0}}{\sin(nx)} + \innerp{\sum_{k=1}^{\infty} a_{k} \cos(kx)}{\sin(nx)} + \innerp{\sum_{k=1}^{\infty} b_{k}\sin(kx)}{\sin(nx)} \quad (\because 内積の線形性) \\
&= \frac{1}{2} a_{0} \innerp{1}{\sin(nx)} + \sum_{k=1}^{\infty} \innerp{a_{k}\cos(kx)}{\sin(nx)} + \sum_{k=1}^{\infty} \innerp{b_{k}\sin(kx)}{\sin(nx)} \quad (\because 内積の線形性) \\
&= \frac{1}{2} a_{0} \innerp{\cos(0)}{\sin(nx)} + \sum_{k=1}^{\infty} a_{k} \innerp{\cos(kx)}{\sin(nx)} + \sum_{k=1}^{\infty} b_{k} \innerp{\sin(kx)}{\sin(nx)} \\
&= \pi b_{n} \quad (\because 三角関数の直交性)
\end{align*}
よって、
\begin{equation*}
b_{n} = \frac{1}{\pi} \innerp{f(x)}{\sin(nx)} \tag{7}
\end{equation*}
全く同様にして \(\innerp{f(x)}{\cos(nx)} \ n \in \mathbb{N}\) を計算することで、次の結果が得られる 。
\begin{equation*}
a_{n} = \frac{1}{\pi} \innerp{f(x)}{\cos(nx)} \tag{8}
\end{equation*}
式7, 式8 の結果を見ると、 係数を取り出すには、関数基底と内積を取って、基底のノルムで割れば良い 事が分かる。
収束定理
いよいよ問題の核心について考えることが出来る。上記までの議論で、三角関数は基底をなすことが示された 。それでは、三角関数によって構築された基底(三角関数基底)は、如何なる関数でも表現できるのだろうか?というのが次の疑問となる。
この疑問に対する答えがフーリエ級数の 収束定理 (以下、単純に収束定理)である。収束定理とは、次の有限項のフーリエ級数展開
\begin{equation*}
S_{N}(x) = \frac{1}{2} a_{0} + \sum_{n=1}^{N} \left\{ a_{n} \cos(nx) + b_{n} \sin(nx) \right\} \tag{9}
\end{equation*}
を用いて信号 \(f(x)\) を近似(\(S_{N}(x) \approx f(x)\) )することを考え、\(N\) の極限 \(N \to \infty\) を取った時に、\(S_{N}(x)\) と \(f(x)\) が一致する、というものである。
\begin{equation*}
\lim_{N \to \infty} \left\{ S_{N}(x) - f(x) \right\} = 0 \tag{10}
\end{equation*}
式10 が証明されれば、理論的観点から、安心してフーリエ級数を使用できると言って良い。ここで、予め注意してほしいのが、式10 の \(f(x)\) は任意の関数では成立せず、定理が成り立つための制約条件が存在することである。
以下、収束定理の証明及び、 \(f(x)\) に課すべき制約条件を見ていく。
ディリクレ核
収束定理 式10 が成立することを示すため、まず有限項のフーリエ級数展開の 式9 に注目する。 式9 の各フーリエ係数 \(a_{0}, a_{1}, ..., b_{1}, b_{2}, ...\) は、 式7, 式8 により、近似対象の関数 \(f(x)\) によって表すことが出来る。
\begin{align*}
S_{N}(x)
&= \frac{1}{2} a_{0} + \sum_{n=1}^{N} \left\{ a_{n} \cos(nx) + b_{n} \sin(nx) \right\} \\
&= \frac{1}{2} \frac{1}{\pi} \innerp{1}{f(x)} + \sum_{n=1}^{N} \left\{ \frac{1}{\pi} \innerp{\cos(ny)}{f(y)} \cos(nx) + \frac{1}{\pi} \innerp{\sin(ny)}{f(y)} \sin(nx) \right\} \\
&= \frac{1}{2\pi} \int_{-\pi}^{\pi} f(y) dy + \sum_{n=1}^{N} \left\{ \frac{1}{\pi} \int_{-\pi}^{\pi} \cos(ny)f(y) dy \cos(nx) + \frac{1}{\pi} \int_{-\pi}^{\pi} \sin(ny)f(y) dy \sin(nx) \right\} \\
&= \frac{1}{\pi} \int_{-\pi}^{\pi} f(y) \left[ \frac{1}{2} + \sum_{n=1}^{N} \left\{ \cos(ny)\cos(nx) + \sin(ny)\sin(nx) \right\} \right] dy \\
&= \frac{1}{\pi} \int_{-\pi}^{\pi} f(y) \left[ \frac{1}{2} + \sum_{n=1}^{N} \cos\left\{n(y-x)\right\} \right] dy \quad (\because \cos の加法定理を使用)
\end{align*}
ここで、 \(z=y-x\) と積分の変数変換を行う。積分範囲は \([-\pi,\pi]\) から \([-\pi-x,\pi-x]\) に変化するが、周期関数を1周期分積分している状態で、積分範囲を左右にずらしても積分の結果は変わらないため、次の結果が得られる。
\begin{align*}
S_{N}(x)
&= \frac{1}{\pi} \int_{-\pi}^{\pi} f(z+x) \left[ \frac{1}{2} + \sum_{n=1}^{N} \cos(nz) \right] dz \\
&= \frac{1}{\pi} \int_{-\pi}^{\pi} f(z+x) D_{N}(z) dz \tag{11}
\end{align*}
式11 で導入した
\begin{equation*}
D_{N}(x) = \frac{1}{2} + \sum_{n=1}^{N} \cos(nx) \tag{12}
\end{equation*}
を ディリクレ核(Dirichlet kernel) という。以下に述べるように、ディリクレ核にはいくつか重要な性質がある。
ディリクレ核の一周期分の積分
定義 式12 より明らかにディリクレ核は周期関数である。周期 \(2\pi\) の積分を実行すると、
\begin{align*}
\int_{-\pi}^{\pi} D_{N}(x) dx
&= \int_{-\pi}^{\pi} \left\{ \frac{1}{2} + \sum_{n=1}^{N} \cos(nx) \right\} dx \\
&= \int_{-\pi}^{\pi} \frac{1}{2} dx + \int_{-\pi}^{\pi} \sum_{n=1}^{N} \cos(nx) dx
= \int_{-\pi}^{\pi} \frac{1}{2} dx + \sum_{n=1}^{N} \int_{-\pi}^{\pi} \cos(nx) dx \\
&= \int_{-\pi}^{\pi} \frac{1}{2} dx \quad (\because 三角関数の一周期分の積分値は0) \\
&= \frac{2\pi}{2} = \pi \tag{13}
\end{align*}
ディリクレ核のsin関数による表現
ディリクレ核は、若干技巧的ではあるが、和を持たない形式に変形することができる。\(D_{N}(x)\) の左から \(2\sin\left(\frac{1}{2}x\right)\) を乗じると、
\begin{align*}
2\sin\left(\frac{1}{2}x\right) D_{N}(x)
&= 2\sin\left(\frac{1}{2}x\right) \left[ \frac{1}{2} + \sum_{n=1}^{N} \cos(nx) \right] \\
&= \sin\left(\frac{1}{2}x\right) + 2\sin\left(\frac{1}{2}x\right) \cos(x) + 2\sin\left(\frac{1}{2}x\right) \cos(2x) + ... + 2\sin\left(\frac{1}{2}x\right) \cos(Nx)
\end{align*}
ここで、三角関数の和の公式 \(\sin(nx)\cos(mx) = \frac{\sin\{(n+m)x\} + \sin\{(n-m)x\}}{2}\) を用いれば、
\begin{align*}
2\sin\left(\frac{1}{2}x\right) D_{N}(x)
&= \sin\left(\frac{1}{2}x\right) + \left[ \sin\left\{\left(\frac{1}{2} - 1\right)x\right\} + \sin\left\{\left(\frac{1}{2} + 1\right)x\right\} \right] \\
&\quad + \left[ \sin\left\{\left(\frac{1}{2} - 2\right)x\right\} + \sin\left\{\left(\frac{1}{2} + 2\right)x\right\} \right] + ... + \left[ \sin\left\{\left(\frac{1}{2} - N\right)x\right\} + \sin\left\{\left(\frac{1}{2} + N\right)x\right\} \right] \\
&= \sin\left(\frac{1}{2}x\right) + \sin\left(-\frac{1}{2}x\right) + \sin\left(\frac{3}{2}x\right) \\
&\quad + \sin\left(-\frac{3}{2}x\right) + \sin\left(\frac{5}{2}x\right) + ... + \sin\left\{\left(\frac{1}{2} - N\right)x\right\} + \sin\left\{\left(\frac{1}{2} + N\right)x\right\} \\
&= \sin\left\{\left(\frac{1}{2} + N\right)x\right\}
\end{align*}
従って、ディリクレ核を \(\sin\) のみで表現することが出来る:
\begin{equation*}
D_{N}(x) = \frac{\sin\left\{\left(\frac{1}{2} + N\right)x\right\}}{2\sin\left(\frac{1}{2}x\right)} \tag{14}
\end{equation*}
ディリクレ核の畳み込み
式11 を改めて眺めると、この式は積分範囲 \([-\pi,\pi]\) において 関数にディリクレ核を畳み込んでいる 式に捉え直せる。
\begin{equation*}
S_{N}(x) = \frac{1}{\pi} \ f(x) \ast D_{N}(x)
\end{equation*}
先取りして収束定理が成り立つと仮定すると、\(N\) の極限 \(N \to \infty\) に於いて次が成り立つ:
\begin{align*}
\lim_{N \to \infty} S_{N}(x) &= \lim_{N \to \infty} \frac{1}{\pi} \ f(x) \ast D_{N}(x) = f(x) \\
\therefore \lim_{N \to \infty} f(x) \ast D_{N}(x) &= \pi f(x)
\end{align*}
畳み込みの結果、畳込み対象の関数 \(f(x)\) が表れている。即ちこの結果は、 \(N\) の極限においてディリクレ関数はインパルス関数に近い振る舞いをすることを示している。
リーマン・ルベーグの補題
収束定理の証明のためには、もう一つ リーマン・ルベーグの補題 なる命題が必要である。この節では、リーマン・ルベーグの補題の証明を行う。
- リーマン・ルベーグの補題
区分的に連続な関数 \(f(x)\) と \(\sin(Nx)\) の積を積分区間 \([a,b]\) で積分したものは、\(N \to \infty\) とすると \(0\) に収束する。
\begin{equation*}
\lim_{N \to \infty} \int_{a}^{b} f(x) \sin(Nx) dx = 0 \tag{15}
\end{equation*}
(証明)部分積分を用いることにより、
\begin{align*}
\int_{a}^{b} f(x) \sin(Nx) dx
&= \int_{a}^{b} f(x) \left\{ -\frac{1}{N} \cos(Nx) \right\}^{\prime} dx \\
&= \left[ -\frac{1}{N} f(x) \cos(Nx) \right]_{a}^{b} - \int_{a}^{b} -\frac{1}{N} f^{\prime}(x) \cos(Nx) dx \quad (\because 部分積分) \\
&= -\frac{1}{N} \left[ f(x) \cos(Nx) \right]_{a}^{b} + \frac{1}{N} \int_{a}^{b} f^{\prime}(x) \cos(Nx) dx
\end{align*}
と変形できる。このまま \(N \to \infty\) なる極限をとれば、いずれの項も \(0\) に収束するように見える。しかしそれは 関数 \(f(x)\) の微分 \(f^{\prime}(x)\) が区間 \([a,b]\) で発散しない(区分的なめらかな)ときのみ 真である。この条件を関数 \(f(x)\) に付加した時、命題は成立する。
では一般に、 \(f(x)\) が区分的に連続であること のみ を仮定して証明を行う。この時は区分的なめらかな関数 \(g(x)\) を用いて命題が成立することを用いて、\(f(x)\) を \(g(x)\) に近づけることで命題の成立を示す。積分区間 \([a,b]\) を \(M\) 分割し、区間の小さい方から順に \(x_{1}, x_{2}, ..., x_{M}\) となるようにする(当然 \(x_{1} = a, x_{M} = b\) が成立する)。この上で \(f(x)\) を次のように構成する:
\begin{equation*}
f(x) = g(x_{k+1}) \quad (k = 1,...,M-1, \ x_{k} \leq x \leq x_{k+1})
\end{equation*}
構成法から見えるように、分割数 \(M\) を増やしていけば、\(f(x)\) と \(g(x)\) の差は小さくなっていくのが分かる(TODO:図を書こう)。即ち、任意の \(\varepsilon > 0\) に対して、 \(|f(x) - g(x)| < \varepsilon\) を成立させる \(M\) が存在する。
そしてこの \(f(x)\) を用いたとき、
\begin{align*}
\left| \int_{a}^{b} f(x) \sin(Nx) dx \right|
&= \left| \int_{a}^{b} \left\{ f(x) - g(x) + g(x) \right\} \sin(Nx) dx \right| \\
&\leq \left| \int_{a}^{b} \left\{ f(x) - g(x) \right\} \sin(Nx) dx \right| + \left| \int_{a}^{b} g(x) \sin(Nx) dx \right| \\
&\leq \int_{a}^{b} \left| f(x) - g(x) \right| \left| \sin(Nx) \right| dx + \left| \int_{a}^{b} g(x) \sin(Nx) dx \right| \\
&\leq \int_{a}^{b} \left| f(x) - g(x) \right| dx + \left| \int_{a}^{b} g(x) \sin(Nx) dx \right| \\
&< \int_{a}^{b} \varepsilon dx + \left| \int_{a}^{b} g(x) \sin(Nx) dx \right| = \varepsilon(b - a) + \left| \int_{a}^{b} g(x) \sin(Nx) dx \right|
\end{align*}
ここで、 \(\displaystyle\left| \int_{a}^{b} g(x) \sin(Nx) dx \right| < \varepsilon\) となる様に \(N\) を十分大きく取る( \(g(x)\) は区分的なめらかなので成立する)と、
\begin{equation*}
\left| \int_{a}^{b} f(x) \sin(Nx) dx \right| < \varepsilon(b-a) + \varepsilon = \varepsilon(b - a + 1)
\end{equation*}
即ち、任意の \(\varepsilon\) に対して上式を成り立たせる \(N\) が存在するので、 式16 が成り立つ。
\begin{equation*}
\lim_{N \to \infty} \left| \int_{a}^{b} f(x) \sin(Nx) dx \right| = 0 \tag{16}
\end{equation*}
式16 は、リーマン・ルベーグの補題( 式15 )が成立していることをそのまま示している。何故なら、ある関数の絶対値が \(0\) に収束することと、関数が \(0\) に収束することは同値だからである。
収束定理の証明
ここまでの結果を利用して、収束定理を示そう。まず 式11 より、ディリクレ核を使用して \(S_{N}(x)\) を書き直すと、
\begin{equation*}
S_{N}(x) - f(x) = \frac{1}{\pi} \int_{-\pi}^{\pi} f(x+z) D_{N}(x) dx - f(x)
\end{equation*}
ここで、ディリクレ核の性質( 式13, 式14 )を用いると、
\begin{align*}
S_{N}(x) - f(x)
&= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x+z) D_{N}(z) dz - 1 \times f(x) \\
&= \frac{1}{\pi} \int_{-\pi}^{\pi} f(x+z) D_{N}(z) dz - \frac{1}{\pi} \int_{-\pi}^{\pi} D_{N}(z) dz f(x) \\
&= \frac{1}{\pi} \int_{-\pi}^{\pi} \left\{ f(x+z) - f(x) \right\} D_{N}(z) dz \\
&= \frac{1}{\pi} \int_{-\pi}^{\pi} \left\{ f(x+z) - f(x) \right\} \frac{\sin\left\{\left( \frac{1}{2} + N \right)z\right\}}{2\sin\left(\frac{1}{2}z\right)} dz \\
&= \frac{1}{\pi} \int_{-\pi}^{\pi} \frac{ f(x+z) - f(x) }{2\sin\left(\frac{1}{2}z\right)} \sin\left\{\left( \frac{1}{2} + N \right)z\right\} dz
\end{align*}
ここでリーマン・ルベーグの補題を用いる。ただし、そのためには、\(\displaystyle\frac{ f(x+z) - f(x) }{2\sin\left(\frac{1}{2}z\right)}\) が区分的に連続でなければならない。この分数は \(z = 0\) の時、分母 \(2\sin\left(\frac{1}{2}z\right)\) が \(0\) になるので、\(z=0\) においても発散しないことを示す必要がある。以下の極限を考えると、
\begin{align*}
\lim_{z \to 0} \frac{ f(x+z) - f(x) }{2\sin\left(\frac{1}{2}z\right)}
&= \lim_{z \to 0} \frac{ f(x+z) - f(x) }{z} \frac{z}{2\sin\left(\frac{1}{2}z\right)} \\
&= \lim_{z \to 0} \frac{ f(x+z) - f(x) }{z} \lim_{z \to 0} \frac{\ddiff{z}{z}}{\ddiff{2\sin\left(\frac{1}{2}z\right)}{z}} \quad (\because ロピタルの定理) \\
&= \lim_{z \to 0} \frac{ f(x+z) - f(x) }{z} \frac{1}{2\frac{1}{2}} \\
&= f^{\prime}(x)
\end{align*}
より、 \(f^{\prime}(x)\) が発散しない、即ち 関数 \(f(x)\) が区分的になめらか であれば、リーマン・ルベーグの補題を使用することで、収束定理
\begin{equation*}
\lim_{N \to \infty} \left\{ S_{N}(x) - f(x) \right\} = 0
\end{equation*}
が成立する。
三角関数の完全性
フーリエ級数の収束定理を用いることで、三角関数基底によって基底は全て揃うのか?という問に答えを与える事ができる。この性質を、 三角関数の完全性 という。
- 三角関数の完全性
- 定数、\(\sin\) 、\(\cos\) によって全ての関数基底が揃っている。
証明は背理法による。
(証明)基底が揃っていない場合には次の仮定が成り立つ。
- 仮定
- 定数、\(\sin\) 、\(\cos\) の全てに直交している連続関数基底が存在する。
この命題の矛盾を導くことで、三角関数基底の完全性を示す。
まず、「定数、sin、cosの全てに直交している連続関数」を \(h(x)\) とおく。その定義から、以下が成り立つ:
\begin{align*}
\ifdiv{ll}{
\innerp{h(x)}{1} = \displaystyle\int_{-\pi}^{\pi} h(x) dx = 0 & \\
\innerp{h(x)}{\cos(nx)} = \displaystyle\int_{-\pi}^{\pi} h(x) \cos(nx) dx = 0 & (n \in \mathbb{N}) \\
\innerp{h(x)}{\sin(nx)} = \displaystyle\int_{-\pi}^{\pi} h(x) \sin(nx) dx = 0 & (n \in \mathbb{N})
}
\end{align*}
これらの条件を満たす自明な関数に \(h(x) = 0\) があるが、 \(h(x) = 0\) は関数空間の零ベクトルに対応し空間を生成しない(この関数をスカラー倍しても同じ関数しか出てこない)ため、基底とはならない。従って、 \(h(x) = 0\) 以外の関数で考える。
この前提の上で、\(h(x)\) をフーリエ係数展開 \(S_{N}(x)\) によって表現すると、
\begin{align*}
S_{N}(x)
&= \frac{1}{2} a_{0} + \sum_{n=1}^{N} \left\{ a_{n} \cos(nx) + b_{n} \sin(nx) \right\} \\
&= \frac{1}{2} \frac{1}{\pi} \innerp{1}{h(x)} + \sum_{n=1}^{N} \left\{ \frac{1}{\pi} \innerp{\cos(ny)}{h(y)} \cos(nx) + \frac{1}{\pi} \innerp{\sin(ny)}{h(y)} \sin(nx) \right\} \\
&= \frac{1}{2\pi} \int_{-\pi}^{\pi} h(y) dy + \sum_{n=1}^{N} \left\{ \frac{1}{\pi} \int_{-\pi}^{\pi} \cos(ny)h(y) dy \cos(nx) + \frac{1}{\pi} \int_{-\pi}^{\pi} \sin(ny)h(y) dy \sin(nx) \right\} \\
&= 0
\end{align*}
フーリエ級数の収束定理を用いると、 \(\displaystyle\lim_{N \to \infty} S_{N} = h(x) = 0\) 。この結果は、 \(h(x) = 0\) 以外の関数で考えていることに矛盾する。従って、冒頭で述べた三角関数の完全性が成り立つ。
フーリエ変換
周期 \(T\) の実関数 \(f : \mathbb{R} \to \mathbb{R}\) に対して、 (複素)フーリエ級数展開は、
\begin{equation*}
\left\{ \begin{array}{l}
f(t) = \displaystyle\sum_{n = -\infty}^{\infty} c_{n} \exp(j n\omega_{0}t) \\
c_{n} = \displaystyle\frac{1}{T} \int^{T/2}_{-T/2} f(t) \exp(-j n\omega_{0} t) dt
\end{array} \right.
\end{equation*}
となる。 ここで \(j\) は虚数単位(\(j = \sqrt{-1}\) )、 \(\omega_{0} = 2\pi/T\) である。 フーリエ級数展開により、 様々な周期関数 \(f\) は周波数領域(異なる周波数を持つ三角関数の和)で表現できることは周知である。 今、 \(c_{n}\) を消去すると、
\begin{equation*}
f(t) = \sum_{n=-\infty}^{\infty} \frac{1}{T} \left\{ \int^{T/2}_{-T/2} f(t) \exp(-jn\omega_{0}t)dt \right\} \exp(jn\omega_{0}t)
\end{equation*}
更に、 \(F(n\omega_{0}) = \displaystyle\int^{T/2}_{-T/2} f(t) \exp(-jn\omega_{0}t) dt\) とおくと、
\begin{equation*}
f(t) = \sum_{n=-\infty}^{\infty} \frac{1}{T} F(n\omega_{0}) \exp(jn\omega_{0}t) = \frac{1}{2\pi} \sum_{n=-\infty}^{\infty} \omega_{0} F(n\omega_{0}) \exp(j n \omega_{0}t)
\end{equation*}
となる。 今、 \(T \to \infty\) ならしめ周期を無限大にすると \(\omega_{0}\) は \(0\) に収束するので、\(\omega_{0}\) を区間幅とした区分求積法により、 次の積分と等しくなる:
\begin{equation*}
\left\{ \begin{array}{l}
f(t) = \displaystyle\frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega) \exp(j \omega t) d\omega \\
F(\omega) = \displaystyle \int^{\infty}_{-\infty} f(t) \exp(-j\omega t) dt
\end{array} \right.
\end{equation*}
ここで \(F(\omega)\) は \(f(t)\) のフーリエ変換、 \(f(t)\) は \(F(\omega)\) のフーリエ逆変換(逆フーリエ変換)と呼ばれる。 非周期的な関数は周期無限の関数とも考えられるので、 フーリエ変換によって、 様々な関数の周波数領域表現を得る事ができる。 但し、\(F(\omega)\) の収束を保証するため、 \(f(t)\) は絶対可積分:
\begin{equation*}
\int_{-\infty}^{\infty} |f(t)| dt < \infty \quad ((-\infty、 \infty)における積分値が有界)
\end{equation*}
でなくてはならない。 もし、 上の積分が有界な値を取るならば、
\begin{align*}
F(\omega)
&= \int^{\infty}_{-\infty} f(t) \exp(-j\omega t) dt \\
&< \int^{\infty}_{-\infty} |f(t) \exp(-j\omega t)| dt < \int^{\infty}_{-\infty} |f(t)||\exp(-j\omega t)| dt \\
&= \int^{\infty}_{-\infty} |f(t)| dt \quad (\because オイラーの公式より |\exp(-j\omega t)| = \sqrt{\cos^{2} \omega t + \sin^{2} \omega t} = 1)
\end{align*}
となって \(F(\omega)\) もまた有界である事が分かる。
ラプラス変換
実関数 \(f(t)\) に収束因子 \(\exp(-\sigma t)\) (\(\sigma\) は非負実数)を乗じた関数 \(f(t)\exp(-\sigma t)\) のフーリエ変換
\begin{equation*}
\int^{\infty}_{-\infty} f(t)\exp(-\sigma t) \exp(-j\omega t) dt = \displaystyle \int^{\infty}_{-\infty} f(t)\exp(-st) dt = F(s) \quad (s = \sigma + j\omega)
\end{equation*}
を (両側)ラプラス変換 と呼ぶ。 ラプラス変換は、 \(s\) が複素数であることにより、 周波数領域だけ(\(\sigma = 0\) とした時。 フーリエ変換と等価となる)でなく、 複素数領域で過渡的な(振動の減衰/増大)現象をも解析の対象とすることができる。 また、\(F(s)\) から \(f(t)\) に変換するラプラス逆変換(逆ラプラス変換)は、 次の式で定義される:
\begin{equation*}
f(t) = \frac{1}{2\pi j} \lim_{\omega \to \infty} \int^{c + j\omega}_{c - j\omega} F(s) \exp(st) ds
\end{equation*}
以後、 実関数 \(f(t)\) のラプラス変換を \(\mathcal{L}[f(t)]( = F(s))\) 、\(F(s)\) のラプラス逆変換を \(\mathcal{L}^{-1}[F(s)]( = f(t))\) と表す。
工学的な応用の場面では、 ラプラス変換の積分範囲は \([0, \infty)\) とする事が多い:
\begin{equation*}
F(s) = \int^{\infty}_{0} f(t)\exp(-st) dt
\end{equation*}
これを特に片側ラプラス変換と呼ぶ。 ラプラス変換は演算子法の一種であり、 様々な関数の変換結果(ラプラス変換対)をまとめたラプラス変換表を参照しながら、 微分方程式を代数的、 かつ簡易に解くことができる。
伝達関数
1つの入力かつ1つの出力があるシステム(一入力一出力システム)を考える。 入力の振る舞いを表す実関数を \(x(t)\) 、 それに対する出力も実関数 \(y(t)\) と表せるとする。 ここで``振る舞いを表す実関数''とは、 線形微分方程式で記述されているラプラス変換可能な関数を意味する。 従って \(x(t), y(t)\) のラプラス変換 \(X(s)、 Y(s)\) は、 微分演算子の存在によりそれぞれ \(s\) の多項式で表現できる事が分かる。
そして、 出力と入力のラプラス変換の比を 伝達関数(Transfer function) と呼ぶ。 伝達関数を \(G(s)\) とすると、
\begin{equation*}
G(s) = \frac{Y(s)}{X(s)}
\end{equation*}
と表すことができる。 伝達関数 \(G(s)\) は入力と出力の関係をひとまとめにし、 システムの特性(性質)を代表している事が分かる。 出力 \(y(t)\) の振る舞いは \(Y(s) = G(s)X(s)\) から両辺ラプラス逆変換を施すことにより求めることができる。 また、 \(G(s)\) 自体の様子(分母分子の多項式の係数)から、 システムの安定性を判定することもできる。 この様に、 伝達関数はシステムの特性を観察する際に大いに役立ち、 古典制御理論の中心をなす概念となっている。
安定性解析の概要
伝達関数からシステムの安定性を解析する事を考える。 まず、 システムが 安定(stable) であるとは、 任意の時間で有界な任意の入力 \(x(t)\) (\({}^{\forall} t. |x(t)| < \infty\) )に対して、 その出力 \(y(t)\) もまた任意の時間で有界である時を言う 。
逆に安定で無い、 即ち出力が有界でない時間がある(\({}^{\exists} t. |y(t)| = \infty\) )システムを不安定(unstable)と言う。 任意の入力 \(x(t)\) に対してその出力 \(y(t)\) の挙動を調べる事は不可能だが、 実際には、 入力 \(x(t)\) を単位ステップ関数
\begin{equation*}
x(t) =
\left\{ \begin{array}{ll}
0 & t < 0 \\
1 & t \geq 0
\end{array} \right.
\end{equation*}
とした時の出力 \(y(t)\) が有界な値に収束すれば安定となる事が示されている。
それでは伝達関数 \(G(s)\) からシステムの安定性を判定する事を考える。 入力 \(x(t)\) 、 出力 \(y(t)\) それぞれのラプラス変換の結果を \(\mathcal{L}[x(t)] = X(s)\) 、 \({\cal L}[y(t)] = Y(s)\) とした時、 伝達関数は \(s\) の多項式の比なので、一般に次の形で表せる:
\begin{align*}
G(s)
&= \frac{Y(s)}{X(s)} = \frac{b_{m}s^{m} + b_{m-1}s^{m-1} + \dots + b_{1}s + b_{0}}{s^{n} + a_{n-1}s^{n-1} + \dots + a_{1}s + a_{0}} \\
&= \frac{b_{m}(s-z_{1})(s-z_{2})\dots(s-z_{m})}{(s-p_{1})(s-p_{2})\dots(s-p_{n})}
\end{align*}
(現実には \(n \geq m\) であることが多く、 その場合 プロパー であると呼ばれる)。 ここで、 \(Y(s) = 0\) の根 \(z_{1}, \dots, z_{m}\) をこのシステムの零点(zero)、 \(X(s)=0\) の根 \(p_{1}、\dots、p_{n}\) をこのシステムの極(pole)と呼ぶ 。
安定性の判定の為入力を単位ステップ関数とすると、 出力のラプラス変換 \(Y(s)\) は
\begin{equation*}
Y(s) = G(s)X(s) = G(s)\frac{1}{s} = \frac{b_{m}(s-z_{1})(s-z_{2})\dots(s-z_{m})}{s(s-p_{1})(s-p_{2})\dots(s-p_{n})}
\end{equation*}
となり、 この式を部分分数分解すると、 一般に
\begin{equation*}
Y(s) = \frac{A}{s} + \sum_{k=1}^{n} \frac{B_{k}}{s-p_{k}}
\end{equation*}
と表わすことができ(\(A、 B_{k}\) :係数)、 これを両辺ラプラス逆変換することで、 出力の一般解
\begin{equation*}
y(t) = A + \sum_{k=1}^{n} B_{k} \exp(p_{k}t)
\end{equation*}
を得る。 更に \(p_{k}\) は一般に複素数なので、 実数係数 \(\sigma_{k}, \omega_{k}\) を用いて \(p_{k} = \sigma_{k} + j \omega_{k}\) と表し \(y(t)\) を変形すると、
\begin{align*}
y(t)
&= A + \sum_{k=1}^{n} B_{k} \exp[(\sigma_{k} + j \omega_{k})t] \\
&= A + \sum_{k=1}^{n} B_{k} \exp(\sigma_{k}t) (\cos\omega_{k}t + j\sin\omega_{k}t) \quad (\because オイラーの公式)
\end{align*}
となる。 今、 ある \(\sigma_{i}\ (i=1, \dots, n)\) が一つでも正ならば、 時間の極限 \(t\to \infty\) をとると \(y(t)\) は発散してしまい、 システムが不安定となることが分かる。
従って システムが安定となる為には全ての極の実数部が負 (\({}^{\forall} k. \sigma_{k} < 0\) ) となる事が必要十分 であることが分かる。この時は特に \(y(t)\) は \(A\) に収束する(\(\displaystyle\lim_{t \to \infty} y(t) = A\) )ので、 システムは 漸近安定 であると言う。
伝達関数に基づくシステムの安定性解析は、 本質的には以上の様に極の実部を調べることにより行われる。 しかし実際複雑な(\(n, m\) が大きい)システムでは方程式を解き極を計算するのが困難となるので、 方程式を解かずともシステムの安定/不安定を判別する手法が存在する 。
ギブス現象
ギブス現象(Gibbs phenomenon) とは、 不連続な点を含む周期関数のフーリエ級数近似において、 不連続点付近では級数和の絶対値が原関数のとる値の絶対値よりも大きくなってしまう現象のことである。 その原因は、 不連続な関数を連続な関数基底で近似してしまう事による。
ギブス現象の例を数式で観察してみる。 今、不連続点を含む、区分的に連続微分可能な周期 \(T\) の実関数 \(f(x)\) を考える。 その \(N\) 次までの複素フーリエ級数近似 \(S_{N}(x)\) は:
\begin{align*}
S_{N}(x)
&= \sum^{N}_{n = -N} c_{n} \exp(jn\omega_{0}x)\quad (\omega_{0} = \frac{2\pi}{T}) \\
c_{n}
&= \frac{1}{T} \int^{T/2}_{-T/2} f(t)\exp(-jn\omega_{0}t) {\rm dt}
\end{align*}
となる。 ところで、 ギブス現象は不連続点付近で \(S_{N}(x)\) が飛び出る事によって認知される。 \(S_{N}(x)\) が三角関数の和で表現されている事に注目すると、 その飛び出た点は、\(S_{N}(x)\) の極値であると捉える事ができる。 従って、 \(S_{N}(x)\) を \(x\) によって微分すると:
\begin{align*}
\ddiff{}{x}S_{N}(x)
&= \sum_{n = -N}^{N} c_{n} \ddiff{}{x}\exp(jn\omega_{0}x) \quad (\because 項別微分) \\
&= j \omega_{0} \sum^{N}_{n = -N} n c_{n} \exp(jn\omega_{0}x) \\
&= j \omega_{0} \sum^{N}_{n = -N} n c_{n} \left\{ \cos(n\omega_{0}x) + j \sin(n\omega_{0}x) \right\} \quad (\because オイラーの公式) \\
&= j \omega_{0} \sum^{N}_{n = -N} n c_{n} \cos(n\omega_{0}x) - \omega_{0} \sum^{N}_{n = -N} n c_{n} \sin(n\omega_{0}x)
\end{align*}
\(c_{n}\) の実部を \({\rm Re}[c_{n}]\) 、 虚部を \({\rm Im}[c_{n}]\) と表すと、
\begin{align*}
\ddiff{}{x}S_{N}(x)
&= - \omega_{0} \left[ \sum^{N}_{n = -N} n \left\{ {\rm Im}[c_{n}]\cos(n\omega_{0}x) + {\rm Re}[c_{n}]\sin(n\omega_{0}x) \right\} \right. \\
\ & \quad - \left. j \sum^{N}_{n = -N} n \left\{ {\rm Re}[c_{n}]\cos(n\omega_{0}x) + {\rm Im}[c_{n}]\sin(n\omega_{0}x) \right\} \right]
\end{align*}
ここで、 \(c_{-n} = c_{n}^{\ast}\) (\(c_{n}\) の複素共役)を用いると、 \({\rm Im}[c_{-n}] = -{\rm Im}[c_{n}]\) 、 \({\rm Re}[c_{-n}] = {\rm Re}[c_{n}]\) であることより、 以下の様に、 虚部を含まない形に整理できる。
\begin{align*}
\ddiff{}{x}S_{N}(x)
&= - \omega_{0} \left[ \sum^{N}_{n = 1} n \left\{ {\rm Im}[c_{n}]\cos(n\omega_{0}x) + {\rm Re}[c_{n}]\sin(n\omega_{0}x) \right\} \right. \\
\ & \quad + \sum^{N}_{k = 1} (-k) \left\{ {\rm Im}[c_{-k}]\cos(k\omega_{0}x) - {\rm Re}[c_{-k}]\sin(k\omega_{0}x) \right\} \\
\ & \quad - j \sum^{N}_{n = 1} n \left\{ {\rm Re}[c_{n}]\cos(n\omega_{0}x) - {\rm Im}[c_{n}]\sin(n\omega_{0}x) \right\} \\
\ & \quad - j \left. \sum^{N}_{k = 1} (-k) \left\{ {\rm Re}[c_{-k}]\cos(k\omega_{0}x) + {\rm Im}[c_{-k}]\sin(k\omega_{0}x) \right\} \right] \\
&= -2\omega_{0} \sum^{N}_{n=1} n \left\{ {\rm Im}[c_{n}]\cos(n\omega_{0}x) + {\rm Re}[c_{n}]\sin(n\omega_{0}x) \right\}
\end{align*}
\(\displaystyle\ddiff{}{x}S_{N}(x)\) を \(0\) とおくと、 \(n > 0\) より、 極値条件の一つとして
\begin{equation*}
{\rm Im}[c_{n}]\cos(n\omega_{0}x) + {\rm Re}[c_{n}]\sin(n\omega_{0}x) = 0 \quad (n = 1, \cdots, N)
\end{equation*}
があり、 これを \(x\) について解くと、
\begin{equation*}
x = -\frac{1}{n\omega_{0}} \tan^{-1}\left( \frac{ {\rm Im}[c_{n}] }{ {\rm Re}[c_{n}] } \right) \quad (n = 1, \cdots, N)
\end{equation*}
が得られる。
ギブス現象の例として、 今、\(f(t)\) として周期 \(2\pi\) の矩形波を仮定する:
\begin{equation*}
f(t) =
\left\{
\begin{array}{ll}
1 & (0 \leq x < \pi) \\
-1 & (\pi \leq x < 2\pi)
\end{array}
\right.
\end{equation*}
定義のとおり、\(f(t)\) は奇関数であるため \({\rm Re}[c_{n}] = 0\) であり、 また \({\rm Im}[c_{n}]\) は:
\begin{align*}
{\rm Im}[c_{n}]
&= - \frac{1}{2\pi} \int^{\pi}_{-\pi} f(t) \sin(nt) {\rm dt} \quad (\omega_{0} = \frac{2\pi}{2\pi} = 1) \\
&= \frac{1}{n\pi} \left[ \cos(nx) \right]^{\pi}_{0} = - \frac{1}{n\pi} \left\{ 1 - (-1)^{n} \right\}
\end{align*}
この結果より \(\tan^{-1}({\rm Im}[c_{n}]/{\rm Re}[c_{n}])\) を考えると、 \({\rm Im}[c_{n}]/{\rm Re}[c_{n}] \to -\infty\) より、 極値条件は、
\begin{equation*}
x = - \frac{1}{n} \left( - \frac{\pi}{2} \right) = \frac{\pi}{2n} \quad (n = 1、\cdots、N)
\end{equation*}
となる。 この結果を用いて、 不連続点 \(x = 0\) における近似 \(S_{N}(x)\) の値を計算する事を考える。 \(x = 0\) に最も近い極値を与える \(x\) の値は、 \(n = N\) の時、 即ち \(x = \displaystyle\frac{\pi}{2N}\) となるので、
\begin{align*}
S_{N}\left(\frac{\pi}{2N}\right)
&= \sum_{n = -N}^{N} c_{n} \exp\left(j\frac{n\pi}{2N}\right) \\
&= \frac{2}{\pi} \sum_{n = 1}^{N} \frac{1}{n} \{ 1 - (-1)^{n} \} \sin\left(\frac{n\pi}{2N}\right) \\
&= \frac{4}{\pi} \sum_{k = 1}^{N} \frac{1}{2k-1} \sin\left(\frac{2k-1}{2N}\pi \right) \quad(n = 2k - 1) \\
&= \frac{2}{\pi} \frac{\pi}{N} \sum_{k = 1}^{N} \frac{1}{\frac{2k-1}{2N}\pi} \sin\left(\frac{2k-1}{2N}\pi \right)
\end{align*}
ここで区分求積法を用いる。 分割幅 \(|\Delta|\) を \(\displaystyle\frac{\pi}{N}\) とすると、
\begin{align*}
S_{N}\left(\frac{\pi}{2N}\right)
&= \frac{2}{\pi} |\Delta| \sum_{k=1}^{N}\frac{1}{\frac{2k-1}{2}|\Delta|}\sin\left(\frac{2k-1}{2}|\Delta|\right) \\
\therefore \lim_{N\to \infty} S_{N}\left( \frac{\pi}{2N} \right)
&= \frac{2}{\pi} \int^{\pi}_{0} \frac{\sin(y)}{y} {\rm dy} \approx 1.17834\cdots
\end{align*}
従って、 \(N\) の極限をとっても目標値 \(1\) に収束できない事が確認できた。 ここで、
\begin{equation*}
\int^{\pi}_{0} \frac{\sin(y)}{y} {\rm dy} = 1.851937052\cdots
\end{equation*}
の結果はギブス定数を用いている。
エイリアシング(折り返し歪み)
エイリアシングは、 連続値(アナログ)信号をPCで扱うために離散(デジタル)化するA/D変換を行った際や、 デジタル化した画像に縮小処理などのフィルターに掛けた際に発生しうる現象であり、
本来音声や画像には見られなかった干渉縞(偽解像、 モアレ)が発生してしまう。
この現象は、 A/D変換においては標本化(サンプリング)の周波数設定、 フィルター処理においてはフィルターそのものが原因である。
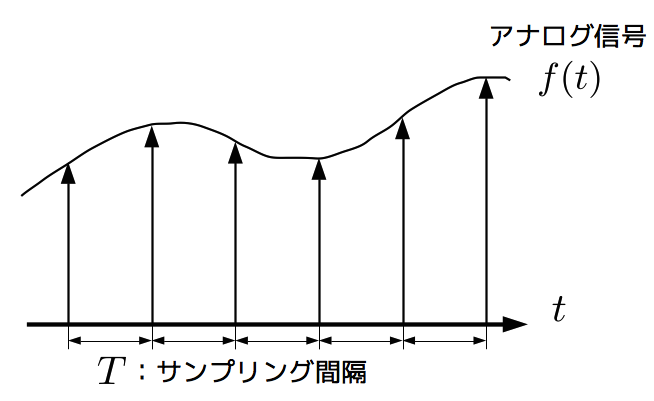
A/D変換におけるエイリアシングの発生の概要を見ていく。 そもそも標本化とは、 連続値信号 \(f(t)\) をある間隔(サンプリング周期) \(T\) での(ディラック)インパルス関数で表現する事を指す( 図1 )。
インパルス関数 \(\delta(t)\) は
\begin{equation*}
\int^{\infty}_{-\infty} f(t)\delta(t) {\rm dt} = f(0)
\end{equation*}
を満たす超関数であり、 標本化信号 \(g(t)\) は、 \(f(t)\) とインパルス関数を周期 \(T\) で並べた周期的デルタ関数 \(\delta_{T}(t)\):
\begin{equation*}
\delta_{T}(t) = \sum^{\infty}_{n = -\infty} \delta(t - nT)
\end{equation*}
との積で表現できる:
\begin{equation*}
g(t) = f(t)\delta_{T}(t) = \sum^{\infty}_{n=-\infty}f(t)\delta(t-nT)
\end{equation*}
数値計算上、 和の無限は扱うことができないので、 ここで信号 \(f(t)\) は、 標本化する区間で周期性を持つと仮定する。 ここでは、 \(f(t)\) はサンプリング間隔の \(N\) 倍の周期 \(NT\) を持つとする:
\begin{equation*}
g(t) = \sum^{N-1}_{n=0}f(t)\delta(t-nT)
\end{equation*}
その仮定の基で、 標本化信号 \(g(t)\) のフーリエ変換 \(\mathcal{F}[g(t)]\) を求めると:
\begin{align*}
\mathcal{F}[g(t)]
&= \int^{\infty}_{-\infty} f(t) \delta_{T}(t) \exp(-j\omega t) {\rm dt} \\
&= \sum^{N-1}_{n = 0} \int^{\infty}_{-\infty} f(t)\delta(t - nT) \exp(-j\omega t) {\rm dt} \\
&= \sum^{N-1}_{n = 0} f(nT) \exp(-jn\omega T)
\end{align*}
ここで$j$は虚数単位、 \(\omega\) は角周波数であり、 この式は離散フーリエ変換(DFT)の式に他ならない。
また、 \(g(t)\) の周波数特性を見やすくするために、 \(\delta_{T}(t)\) をフーリエ級数展開する。 \(\delta_{T}(t)\) の複素フーリエ級数展開の式は:
\begin{align*}
\delta_{T}(t)
&= \sum^{\infty}_{n = -\infty} c_{n} \exp(jn\omega_{0}t) \quad (\omega_{0} = \frac{2\pi}{T}) \\
c_{n}
&= \frac{1}{T} \int^{T/2}_{-T/2} \delta_{T}(t)\exp(-jn\omega_{0}t) {\rm dt}
\end{align*}
\(c_{n}\) を計算するとき、 積分範囲には唯一つのインパルスが存在する事に留意すると、 次のようになる:
\begin{align*}
c_{n}
&= \frac{1}{T} \int^{T/2}_{-T/2} \delta(t)\exp(-jn\omega_{0}t) {\rm dt} \\
&= \frac{1}{T} \exp(0) = \frac{1}{T} \\
\therefore \delta_{T}(t) &=
\frac{1}{T} \sum^{\infty}_{n = -\infty} \exp(jn\omega_{0} t)
\end{align*}
この結果から \(g(t)\) の周波数特性を計算する。 \(\mathcal{F}[f(t)] = F(\omega)\) と書くと、
\begin{align*}
\mathcal{F}[g(t)]
&= \mathcal{F}[f(t) \frac{1}{T} \sum^{\infty}_{n = -\infty} \exp(jn\omega_{0} t)] \\
&= \frac{1}{T} \sum^{\infty}_{n = -\infty} \mathcal{F}[f(t)\exp(jn\omega_{0}t)] \quad (\because フーリエ変換の線形性) \\
&= \frac{1}{T} \sum^{\infty}_{n = -\infty} \int^{\infty}_{-\infty} f(t) \exp\left[ -j(\omega - n\omega_{0})t \right] {\rm dt} \\
&= \frac{1}{T} \sum^{\infty}_{n = -\infty} F(\omega - n\omega_{0})
\end{align*}
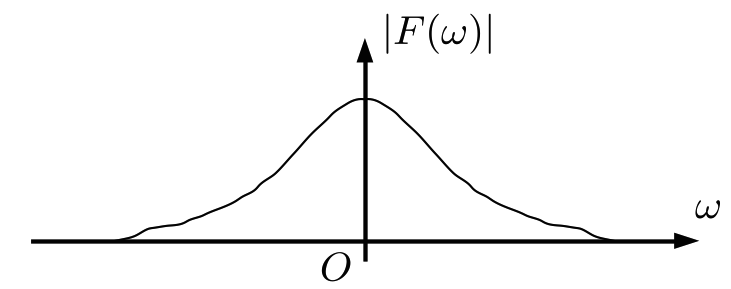
従って、 \(f(t)\) の周波数特性 \(F(\omega)\) を \(\omega_{0}\) ずつずらして和をとったものとなる。 典型的な信号の周波数は高周波成分になるに従って振幅(パワー、 ゲイン)が減衰する事が知られているので、 原信号と離散化信号の周波数スペクトル \(|F(\omega)|\) の概要図は 図2 のようになる。
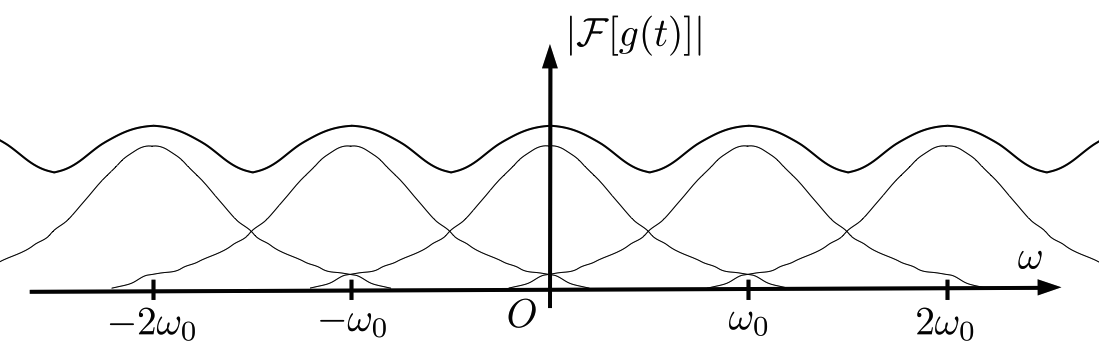
\(|F(\omega)|\) は明らかに偶関数であり、 この時、 \(|{\cal F}[g(t)]|\) のある山 \(|F(\omega - i\omega_{0})|(i \in \mathbb{Z})\) において、 隣の山 \(|F(\omega - (i \pm 1) \omega_{0})|\) と交差する周波数は \(\displaystyle \frac{\omega_{0}}{2}k (k:奇数)\) となる。
すると、 \(|{\cal F}[g(t)]|\) はそれらの山の和を取るので、 結果 \(\displaystyle \frac{\omega_{0}}{2}k \pm \beta\) の周波数成分のパワーが隣の山のスペクトルと区別できなくなってしまう( 図3 )。 特に、原信号 \(f(t)\) では弱かった高周波成分のスペクトルが強調されてしまい、 離散化後の信号においてそれが干渉縞等によって現れてしまう。 この現象をエイリアシングと呼ぶ。
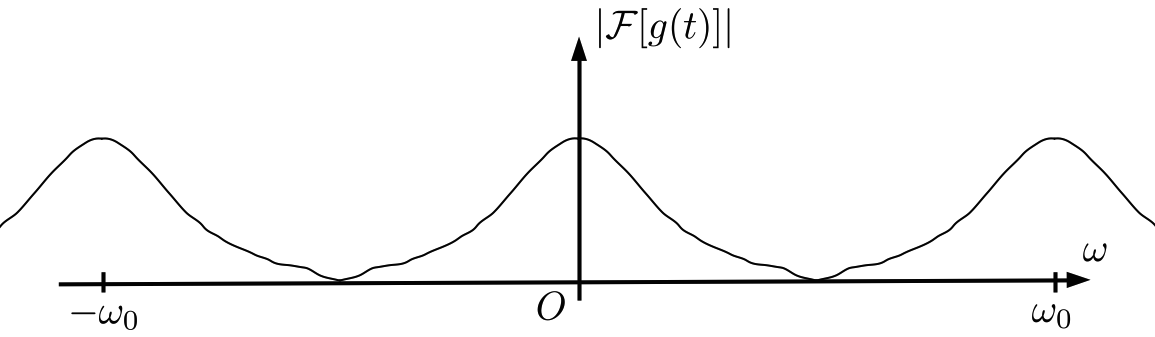
エイリアシングを防ぐには、原理的には、原信号 \(f(t)\) の周波数 \(\omega_{f} = \displaystyle\frac{2\pi}{NT}\) の2倍以上の周波数成分をローパスフィルターなどでカットし、かつ、サンプリング周波数を \(2\omega_{f}\) (ナイキストレート)より大きくとれば良い( 図4 )
信号の復元
フーリエ変換対の結果から、標本化した波形をアナログ信号に一意に復元する結果が得られる。
改めてフーリエ逆変換の結果
\begin{equation*}
f(t) = \frac{1}{2\pi} \int^{\infty}_{-\infty} F(\omega) \exp(j\omega t) d\omega
\end{equation*}
を眺め、その意味をもう一度立ち戻って考えてみると、これは無限の周波数帯域を使用して信号を復元している式にも見える。
この式をサンプリング周波数で帯域制限して信号を復元する事を考えることで、標本化した信号をアナログ信号に復元する式が得られる。
まず フーリエ変換の結果 \(F(\omega)\) を標本化信号によって表すことを考える。区分求積法の援用により、
\begin{align*}
F(\omega) &= \int^{\infty}_{-\infty} f(t) \exp(-j\omega t) dt \\
&= \lim_{f_{s} \to \infty} \sum_{n=-\infty}^{\infty} \frac{1}{f_{s}} f\left(\frac{n}{f_{s}}\right) \exp\left(-j\omega\frac{n}{f_{s}}\right)
\end{align*}
と形式的に表すことが出来る。ここで、\(f_{s}\) はサンプリング周波数(サンプリングレート)である。この結果をフーリエ逆変換の式に代入すると、
\begin{align*}
f(t) &= \frac{1}{2\pi} \int^{\infty}_{-\infty} F(\omega) \exp(j\omega t) d\omega \\
&= \frac{1}{2\pi} \int^{\infty}_{-\infty} \left\{ \lim_{f_{s} \to \infty} \sum_{n=-\infty}^{\infty} \frac{1}{f_{s}} f\left(\frac{n}{f_{s}}\right) \exp\left(-j\omega\frac{n}{f_{s}}\right) \right\} \exp(j\omega t) d\omega \\
&= \frac{1}{2\pi} \lim_{f_{s} \to \infty} \sum_{n=-\infty}^{\infty} \frac{1}{f_{s}} f\left(\frac{n}{f_{s}}\right) \int^{\infty}_{-\infty} \exp\left[j\omega \left( t - \frac{n}{f_{s}} \right) \right] d\omega
\end{align*}
ここで、最後の式変形の所で積分演算の線形性を用いて、和の順序を交換している。得られた最後の結果の積分
\begin{equation*}
\int^{\infty}_{-\infty} \exp\left[j\omega \left( t - \frac{n}{f_{s}} \right) \right] d\omega
\end{equation*}
に注目する。積分範囲 \([-\infty, \infty]\) は無限になっているが、実際に得られるスペクトルは、標本化の結果 \([-\omega_{0}/2, \omega_{0}/2]\) の範囲に制限されていなければならない。従って、帯域制限を加味して積分を計算すると、
\begin{align*}
\int^{\omega_{0}/2}_{-\omega_{0}/2} \exp\left[j\omega \left( t - \frac{n}{f_{s}} \right) \right] d\omega &= \frac{1}{j\left( t - \frac{n}{f_{s}} \right)} \left[ \exp \left\{ j\omega\left( t - \frac{n}{f_{s}} \right) \right\} \right]^{\omega_{0}/2}_{-\omega_{0}/2} \\
&= \frac{1}{j\left( t - \frac{n}{f_{s}} \right)} \left[ \exp \left\{ j\frac{\omega_{0}}{2} \left( t - \frac{n}{f_{s}} \right) \right\} - \exp \left\{ -j\frac{\omega_{0}}{2} \left( t - \frac{n}{f_{s}} \right) \right\} \right] \\
&= \frac{1}{j\left( t - \frac{n}{f_{s}} \right)} j2 \sin \left[ \frac{\omega_{0}}{2} \left( t - \frac{n}{f_{s}} \right) \right] = \frac{2 \sin \left[ \pi f_{s} \left( t - \frac{n}{f_{s}} \right) \right]}{t - \frac{n}{f_{s}}}
\end{align*}
ここで、最後の式変形の所でオイラーの公式
\begin{equation*}
\exp(jx) - \exp(-jx) = \cos(x) + j\sin(x) - \left\{ \cos(x) - j\sin(x) \right\} = j2\sin(x)
\end{equation*}
を用いている。続けて、帯域制限を加味した積分結果を代入する。 極限 \(\displaystyle\lim_{f_{s} \to \infty}\) は帯域制限の結果考慮する必要が無くなる事に留意すると、
\begin{align*}
f(t) &= \frac{1}{2\pi} \sum_{n=-\infty}^{\infty} \frac{1}{f_{s}} f\left(\frac{n}{f_{s}}\right) \frac{2 \sin \left[ \pi f_{s} \left( t - \frac{n}{f_{s}} \right) \right]}{t - \frac{n}{f_{s}}} \\
&= \sum_{n=-\infty}^{\infty} f\left(\frac{n}{f_{s}}\right) \frac{\sin \left[ \pi f_{s} \left( t - \frac{n}{f_{s}} \right) \right]}{ \pi f_{s} \left( t - \frac{n}{f_{s}} \right)} \\
&= \sum_{n=-\infty}^{\infty} f\left(\frac{n}{f_{s}}\right) \mathrm{sinc} \left[ f_{s} \left( t - \frac{n}{f_{s}} \right) \right] \tag{17}
\end{align*}
ここで、
\begin{equation*}
\mathrm{sinc}(x) = \frac{\sin(\pi x)}{\pi x}
\end{equation*}
は シンク関数(Sinc function) と呼ばれる。シンク関数の概形は次のようになっており、 \(x=0\) で最大値 \(1\) をとる( \(\because\) ロピタルの定理より、 \(\displaystyle \lim_{x \to 0} \frac{\sin(\pi x)}{\pi x} = \lim_{x \to 0} \frac{\frac{d \sin(\pi x)}{dx}}{\frac{d \pi x}{dx}} = \lim_{x \to 0} \frac{\pi \cos(\pi x)}{\pi} = 1\) )。
式17 の結果から、 元のアナログ信号 \(f(t)\) はシンク関数の畳み込み演算によって完全に復元される事 が示された。