SVM（サポートベクトルマシン）

SVM(Support Vector Machine, サポートベクトルマシン)は、深層学習の影に隠れがちではあるものの、現在使われている識別学習モデルの中でも比較的認識性能が優れ、実用に供される事はもちろん、様々な研究でも比較対象となる手法の一つである。

SVMの大雑把な理論的概要を述べると、SVMは与えられた学習サンプルを最も適切に分離（識別）する境界面（識別面）を発見する手法である。その識別面は凸計画問題に帰着して求める事ができるので、どの様なサンプルにおいても（存在するならば）最適な識別面を構成できる。

本稿では、最初に基本となる線形SVMの定式化を行い、次に汎用性をより高めた非線形SVMとソフトマージンSVMを説明し、最後にSVMを回帰問題に適用したSVR(Support Vector Regression, サポートベクトル回帰)を説明する。最後にC言語による実装例を挙げる。

SVMも知り尽くされており、文献・資料は大量に存在する。ここでは、参考書籍 [1], [2] を挙げる。

線形SVM
- マージンの定式化
- マージン最大化
  - KKT条件
非線形SVM
ソフトマージンSVM
SVR（Support Vector Regression, サポートベクトル回帰）
- 1ノルムSVR・双対問題の導出
- 2ノルムSVR・双対問題の導出
実装の例
- 学習
  - 学習則の導出
  - 実装
- 制約条件の考慮
  - 正例と負例の双対係数の和を等しくする
  - 双対係数は非負
識別
脚注

識別の例として、まずは図にあるような、2次元空間\(X\times Z\)に存在する2クラスのサンプルデータ（以下サンプル）を仮定する。各クラスは二値のラベル付け\(y=\{-1, 1\}\)がなされており、識別面（2次元空間では直線）\(ax+bz+c=0\)の上半領域（\(ax+bz+c>0\)）にラベル\(y=1\)のサンプルが、下半領域（\(ax+bz+c<0\)）にラベル\(y=-1\)のサンプルが分布するようにする。

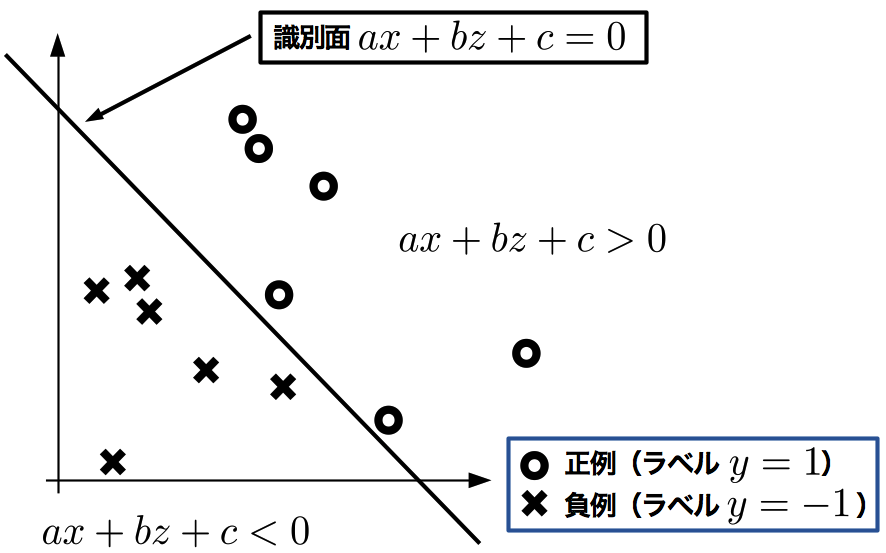
2クラス分離の例

更に、\(n\)次元空間の元（ベクトル）\(\boldsymbol{x} \in \mathbb{R}^{n}\)で表されるサンプルに対しても一般化でき、\(n\)次元の係数ベクトル\(\boldsymbol{w} \in \mathbb{R}^{n}\)を用いることで、識別面は

\begin{equation*} \begin{aligned} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{x} + b = 0 \end{aligned} \end{equation*}

と表現できる。ここで\(b \in \mathbb{R}\)は切片（しきい値、バイアス）である。

概要でも述べたとおり、識別面は異なるラベルが付いたサンプルを互いに分離さえできていれば良いので、識別面の候補は無限に存在してしまう（上の2次元の例でも明らかである）。しかし、その全てが適切な識別面とは限らない。 SVMでは、次の2点を最適な識別面の条件とする。

各クラスの、最も識別面に近いサンプル（サポートベクトル）までの距離を最大にする。
また、その距離を各クラスで同一にする。

この2点を満たす識別面ならば、丁度クラス間の中心を区切ることが出来、適切な識別面といえる。また、図に示す様に、サポートベクトル間の距離をマージン（余白）という。 SVMは、このマージンを最大化することが目的となる。

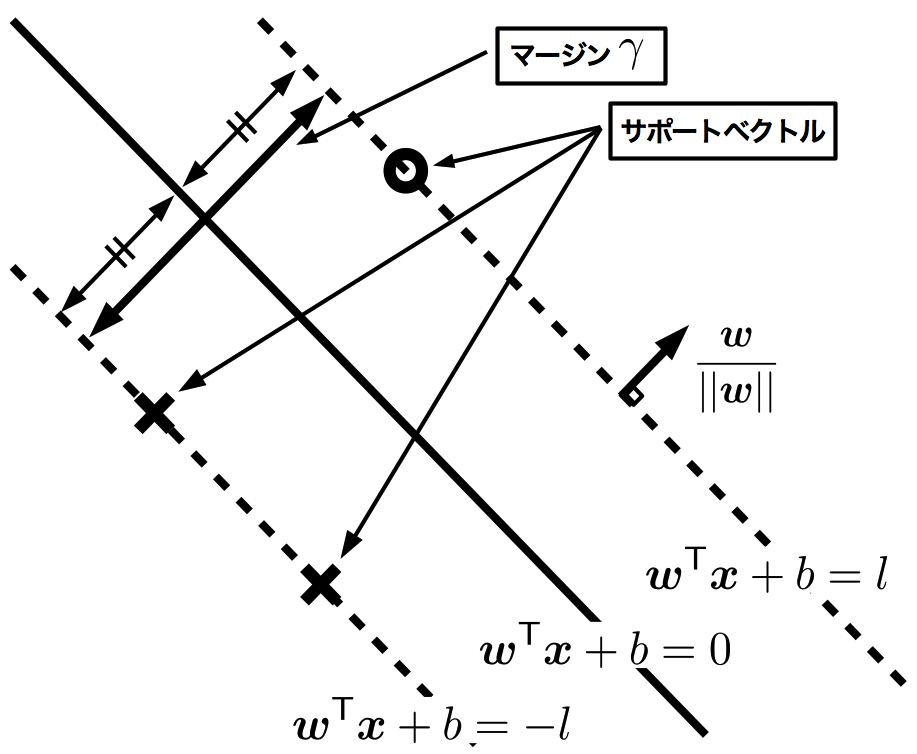
マージン

それでは、マージンの定式化を考える。\(n\)次元空間上に\(N\)個存在するサンプルを\(\boldsymbol{x}\_{i} \in \mathbb{R}^{n} \ (i=1, \dots, N)\)と書き、またそのデータに対応する二値ラベルを\(y_{i} \in \{-1, 1\}\ (i=1, \dots, N)\)とかく。全てのサンプルが正しく識別されている時には、

\begin{equation*} \begin{aligned} y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) \geq 0 \quad (i = 1, \dots, N) \end{aligned} \end{equation*}

が明らかに成立する。そして、異なる2クラスのサポートベクトル\(\boldsymbol{x}\_{s}, \boldsymbol{x}\_{t}\)が

\begin{equation*} \begin{aligned} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{s} + b = l , \quad \boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{t} + b = -l\end{aligned} \end{equation*}

が成立すると仮定する [3] と（\(l>0\)）、 \(\boldsymbol{x}\_{s}\)と\(\boldsymbol{x}\_{t}\)の、識別面に対して平行な距離がマージンとして計算できる。マージンを\(\gamma\)と書くと、平面の単位法ベクトルは\(\boldsymbol{w}/||\boldsymbol{w}||\)（\(||\boldsymbol{w}|| = \sqrt{\boldsymbol{w}^{\mathsf{T}}\boldsymbol{w}}\)）で与えられるので、マージンは

\begin{equation*} \begin{aligned} & \boldsymbol{w}^{\mathsf{T}}(\boldsymbol{x}_{t} + \gamma \frac{\boldsymbol{w}}{||\boldsymbol{w}||}) + b = \boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{s} + b \nonumber \\ &\iff \gamma \frac{\boldsymbol{w}^{\mathsf{T}}\boldsymbol{w}}{||\boldsymbol{w}||} = \gamma ||\boldsymbol{w}|| = (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{s}+b) - (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{t}+b) = 2l \nonumber \\ &\therefore \gamma = \frac{2l}{||\boldsymbol{w}||}\end{aligned} \end{equation*}

で求められる。

マージン最大化

前節でも既に述べたが、 SVMの目的はマージン\(\gamma\)を最大化することである。単純には\(\max \gamma\)と書けるが、最適化を行いやすくするため、\(1/\gamma\)の最小化に置き換え、 \(l\)は最適化に関与しないので\(l=1\)とし、更に\(||\boldsymbol{w}||\)が最小化された時は\(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{w}\)も最小化されるので、考えるべき最適化問題は次のように書ける:

\begin{equation*} \begin{aligned} & \max_{\scriptsize \boldsymbol{w}} \gamma = \frac{2l}{||\boldsymbol{w}||} \quad \text{subject to : } y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) \geq l \nonumber \\ &\implies \min_{\scriptsize \boldsymbol{w}} \frac{1}{2} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{w} \quad \text{subject to : } y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) \geq 1 \quad (i=1, \dots, N)\end{aligned} \end{equation*}

この最適化問題は、凸計画問題 [4] であり、不等式制約付き非線形計画問題なので、 KKT条件(Karush-Kuhn-Tucker condition)を用いる。KKT条件はラグランジェの未定乗数法（等式制約）の一般化であり、次の定理で表される:

KKT条件

\(\boldsymbol{v}^{\star}\)を\(f(\boldsymbol{v})\)に関しての最適化問題の最適解とするならば、次の条件を満たす最適重みベクトル\(\boldsymbol{\alpha}^{\star}=[\alpha_{1}^{\star}, \cdots, \alpha_{N}^{\star}]^{\mathsf{T}}\ (\alpha_{i} \geq 0)\)が存在する。

\begin{equation*} \begin{aligned} \left\{ \begin{array}{ll} \displaystyle\frac{\partial{\cal L}(\boldsymbol{v}^{\star}, \boldsymbol{\alpha}^{\star})}{\partial \boldsymbol{v}} &= 0 \\ \boldsymbol{\alpha}^{\star\mathsf{T}}\boldsymbol{g}(\boldsymbol{v}^{\star}) &= 0 \end{array} \right. \end{aligned} \end{equation*}

ここで\(\boldsymbol{g}(\boldsymbol{v})\)は制約条件式\(\boldsymbol{g}(\boldsymbol{v}) = [g_{1}(\boldsymbol{v}), \cdots, g_{N}(\boldsymbol{v})]^{\mathsf{T}}\), \({\cal L}\)はラグランジアン（ラグランジェ関数）であり以下の様に表される。

\begin{equation*} \begin{aligned} g_{i}(\boldsymbol{v}) &\geq 0\ \ (i = 1, \dots, N) \\ {\cal L}(\boldsymbol{v}, \boldsymbol{\alpha}) &= f(\boldsymbol{v}) + \boldsymbol{\alpha}^{\mathsf{T}}\boldsymbol{g}(\boldsymbol{v}) \end{aligned} \end{equation*}

\({\cal L}\)が凸関数ならば、最適点\((\boldsymbol{v}^{\star}, \boldsymbol{\alpha}^{\star})\)は鞍点にあり、\(\displaystyle\max_{\scriptsize \boldsymbol{v}} {\cal L}(\boldsymbol{v}, \boldsymbol{\alpha}^{\star})\)を主問題とする時、\(\displaystyle\min_{\scriptsize \boldsymbol{\alpha}}{\cal L}(\boldsymbol{v}^{\star}, \boldsymbol{\alpha})\)を主問題に対する双対問題という。 [5]

それでは実際にKKT条件を適用し、最適化問題を主問題(式)から双対問題へ変換する事を考える。まず制約条件から

\begin{equation*} \begin{aligned} g_{i}(\boldsymbol{w}) = 1 - y_{i} (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) \leq 0\end{aligned} \end{equation*}

（最小化を考えているので、符号が逆転している事に注意）より、ラグランジアンは、

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{w}, \boldsymbol{\alpha}) &= \frac{1}{2} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{w} + \boldsymbol{\alpha}^{\mathsf{T}}\boldsymbol{g}(\boldsymbol{w}) \\ &= \frac{1}{2} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{w} + \sum_{i=1}^{N}\alpha_{i} \{ 1 - y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) \}\end{aligned} \end{equation*}

と表現でき、 \({\cal L}(\boldsymbol{w}, \boldsymbol{\alpha})\)の\(\boldsymbol{w}, b\)による偏微分は、

\begin{equation*} \begin{aligned} \frac{\partial {\cal L}(\boldsymbol{w}, \boldsymbol{\alpha})}{\partial \boldsymbol{w}} = \boldsymbol{w} - \sum_{i=1}^{N} \alpha_{i}y_{i}\boldsymbol{x}_{i}, \quad \frac{\partial {\cal L}(\boldsymbol{w}, \boldsymbol{\alpha})}{\partial b} = \sum_{i=1}^{N}\alpha_{i}y_{i}\end{aligned} \end{equation*}

となる。\(\displaystyle\frac{\partial {\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\alpha})}{\partial \boldsymbol{w}} = \boldsymbol{0}\)とおくことで最適時の係数\(\boldsymbol{w}^{\star}\)が求まる:

\begin{equation*} \begin{aligned} \boldsymbol{w}^{\star} = \sum_{i=1}^{N} \alpha_{i}y_{i}\boldsymbol{x}_{i}\end{aligned} \end{equation*}

また、\(\displaystyle\frac{\partial {\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\alpha})}{\partial b} = 0\)により双対変数\(\boldsymbol{\alpha}\)の制約条件が得られる:

\begin{equation*} \begin{aligned} \sum_{i=1}^{N} \alpha_{i}y_{i} = 0\end{aligned} \end{equation*}

これらの関係式をラグランジアンに代入することで、双対問題式を得る:

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{w}^{\star}、 \boldsymbol{\alpha}) &= \frac{1}{2} \boldsymbol{w}^{\star\mathsf{T}}\boldsymbol{w}^{\star} + \boldsymbol{\alpha}^{\mathsf{T}} \boldsymbol{g}(\boldsymbol{w}^{\star}) \\ &= \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\boldsymbol{x}_{j}^{\mathsf{T}}\boldsymbol{x}_{i} + \sum_{i=1}^{N} \alpha_{i} \left\{ 1 - y_{i} \left( \sum_{j=1}^{N}\alpha_{j}y_{j}\boldsymbol{x}_{j}^{\mathsf{T}} \boldsymbol{x}_{i} + b \right) \right\} \\ &= \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\boldsymbol{x}_{i}^{\mathsf{T}}\boldsymbol{x}_{j} + \sum_{i=1}^{N} \alpha_{i} - b\sum_{i=1}^{N} \alpha_{i} y_{i} - \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\boldsymbol{x}_{i}^{\mathsf{T}} \boldsymbol{x}_{j} \\ &= \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\boldsymbol{x}_{i}^{\mathsf{T}}\boldsymbol{x}_{j}\end{aligned} \end{equation*}

（途中の式変形において、内積の対称性（\(\boldsymbol{x}^{\mathsf{T}}\_{j}\boldsymbol{x}\_{i} = \boldsymbol{x}^{\mathsf{T}}\_{i}\boldsymbol{x}\_{j}\)）を用いている。）よって、双対問題は

\begin{equation*} \begin{aligned} & \max_{\scriptsize \boldsymbol{\alpha}} \left[ \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\boldsymbol{x}_{i}^{\mathsf{T}}\boldsymbol{x}_{j} \right] \\ & \text{subject to : } \alpha_{i} \geq 0, \ \sum_{i=1}^{N} \alpha_{i}y_{i} = 0 \quad (i = 1, \dots, N) \nonumber\end{aligned} \end{equation*}

と表現できる。双対問題は非負制約\(\alpha_{i} \geq 0\)の中で\(\boldsymbol{\alpha}\)を動かし、その最大値を得れば良いので、主問題を直接解くよりも容易に、数値最適化によって解を求める（学習する）ことができる。実際の実装については後に述べる。

非線形SVM

前節までの議論は、入力データと同じ空間（次元）で適切な識別面を発見するSVMであり、これを特に線形SVMという。線形SVMの場合、識別面は入力データ空間の次元\(n\)に対し\(n-1\)次元の平面（超平面）であり（例:2次元空間では直線、3次元空間では平面）、図の様に、異なるクラスのサンプルが入り組んだ状態では識別面を構成できない（線形分離不可能）。

線形分離不可能な例

この場合、入力データの空間\(\mathbb{R}^{n}\)から高次元空間\(\mathbb{R}^{h}\)(\(h \gg n\))への高次元な非線形写像（特徴写像）\(\boldsymbol{\phi} : \mathbb{R}^{n} \to \mathbb{R}^{h}\)を用いて高次元空間（特徴空間）へ写像すれば、線形分離不可能だったサンプルを一般位置 [6] に写し、識別面を構成できる（線形分離可能）ようになる（図参照）。

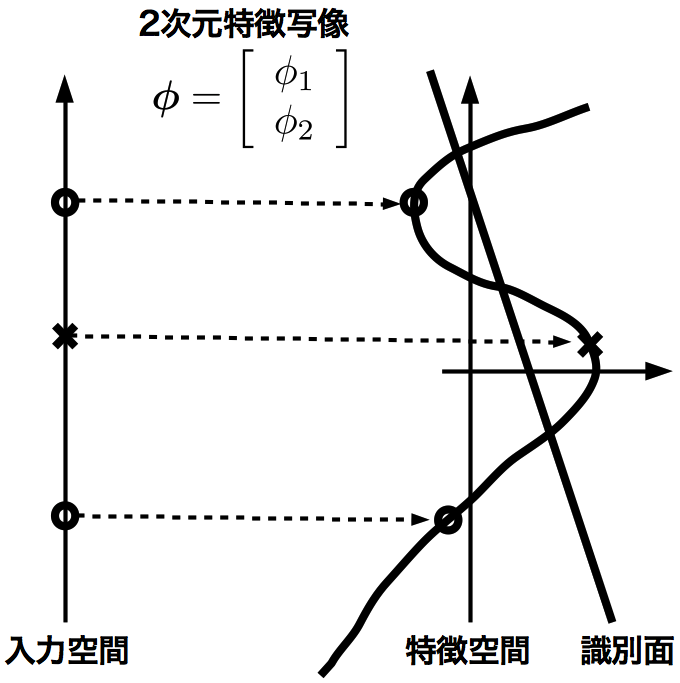
特徴空間で線形分離可能になる例

図では、入力空間は1次元（数直線）、特徴空間は2次元（平面）である。入力空間で線形分離不可能なサンプルが、特徴写像によって一般位置に写され、線形分離可能になっている。

この様に、入力データ次元で線形分離不可能なサンプルを、特徴写像によって写して識別面を構成し、元の次元に戻すSVMを非線形SVMという。この場合、識別面は曲がった形状を持つ（超曲面）。

それでは非線形SVMの定式化を見ていく。特徴写像を用いてサンプルを写像することで、高次元空間内のサンプル（特徴サンプル）\(\boldsymbol{\phi}(\boldsymbol{x}_{i})\ (i =1, \dots, N)\)が得られる。後は線形SVMの時と全く同様の議論を適用し、双対問題は次の様に表現される:

\begin{equation*} \begin{aligned} &\max_{\scriptsize \boldsymbol{\alpha}} \left[ \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\boldsymbol{\phi}(\boldsymbol{x}_{i})^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{j}) \right] \\ &\text{subject to : } \alpha_{i} \geq 0,\ \sum_{i=1}^{N} \alpha_{i}y_{i} = 0 \quad (i = 1, \dots, N) \nonumber\end{aligned} \end{equation*}

さて、この様にして非線形SVMが実現できるが、一般に、入力次元\(n\)はもとより特徴空間の次元\(h\)は非常に大きくなる（\(\infty\)次元にすらなりうる）。特徴写像\(\boldsymbol{\phi}\)を構成する\(h\)個の非線形な基底を用意するのは、非常に困難であり、実用上大変な不便が生じる。そこで、特徴写像同士の内積\(\boldsymbol{\phi}(\boldsymbol{x}\_{i})^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}\_{j})\)の計算結果はノルムなので、その内積を計算するのではなく、天下り的に、最初から内積値を与えてしまうやり方がある。即ち、特徴写像同士の内積値を、 カーネル関数 \(K : \mathbb{R}^{n} \times \mathbb{R}^{n} \to \mathbb{R}\)で定める:

\begin{equation*} \begin{aligned} K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) = \langle \boldsymbol{\phi}(\boldsymbol{x}_{i}), \boldsymbol{\phi}(\boldsymbol{x}_{j}) \rangle = \boldsymbol{\phi}(\boldsymbol{x}_{i})^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{j})\end{aligned} \end{equation*}

ここで\(K\)は入力データのみで記述されるので、特徴写像はカーネル関数の中に閉じ込められてしまい、陽に現れない。即ち、特徴写像を構成する必要がないというのが大きなメリットである。任意の関数がカーネルになるとは限らず、マーサーの定理 [7] という条件をカーネル関数は満たす必要がある。代表的なカーネル関数を以下に挙げる:

線形カーネル:

\begin{equation*} \begin{aligned} K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) = \langle \boldsymbol{x}_{i}, \boldsymbol{x}_{j} \rangle \end{aligned} \end{equation*}

入力次元における標準内積もカーネルとなり、線形カーネルと呼ばれる。

ガウシアン（Radial Basis Function、 RBF:放射基底関数）カーネル:

\begin{equation*} \begin{aligned} K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) = \exp\left(-\frac{||\boldsymbol{x}_{i}-\boldsymbol{x}_{j}||^{2}}{2\sigma^{2}}\right) \end{aligned} \end{equation*}

分散パラメタ\(\sigma\)を伴ってガウス関数に従った分布を示す。実用上よく用いられる。

多項式カーネル:

\begin{equation*} \begin{aligned} K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) = (\langle \boldsymbol{x}_{i}, \boldsymbol{x}_{j} \rangle + c)^{k} \end{aligned} \end{equation*}

正定数\(c\)と多項式の次数\(k\)によって構成されるカーネルである。ガウシアンカーネルよりも性能がパラメタに依存しない特徴を持つ。

カーネル関数\(K\)を用いる事で、非線形SVMの双対問題は次で表される:

\begin{equation*} \begin{aligned} &\max_{\scriptsize \boldsymbol{\alpha}} \left[ \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}K(\boldsymbol{x}_{i}、 \boldsymbol{x}_{j}) \right] \\ &\text{subject to : } \alpha_{i} \geq 0、\ \sum_{i=1}^{N} \alpha_{i}y_{i} = 0 \quad (i = 1, \dots, N) \nonumber\end{aligned} \end{equation*}

ソフトマージンSVM

前節までのSVMは、マージンの内部にサンプルが入る事を一切許さないので、これを特にハードマージンSVMということがある。カーネルを用いた非線形ハードマージンSVMは、線形分離不可能なサンプルにでも強引に曲がりくねった識別面を構成する。これは実用に供する場合に問題になることがある。例えば、データに雑音が乗っていたり、一部のラベルを付け間違えたりする場合であり、これらは実データを扱う場合、往々にして起こりうる事である。この様な雑音を拾いすぎてしまうとSVMの汎化性能 [8] が悪化してしまうので、マージンの制約を緩め、一部のサンプルはマージンの内部に入っても良いようにSVMを改善する事を考える。マージンの内部にサンプルが入ることを許すSVMをソフトマージンSVMと呼ぶことがある。

ハードマージンSVMの制約を緩める事を考える。サンプル\(\boldsymbol{x}\_{i}\)に対応するスラック（緩衝）変数\(\eta_{i} \geq 0\ (i=1, \dots, N)\)を用意して、 SVMの制約を

\begin{equation*} \begin{aligned} y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}\_{i}) + b) \geq 1 - \eta_{i} \quad (i = 1, \dots, N)\end{aligned} \end{equation*}

とする（最初から、サンプルは特徴写像\(\boldsymbol{\phi}\)によって写像されている場合を考える）。スラック変数はサンプルがマージンに食い込んでいる距離を表しており、もちろん、 \(\eta_{i}\)は小さい方が良く、\(\eta_{i} = 0\)の時はハードマージンに一致する。そして、\(\eta_{i}\)も同時に最適化に組み込んでしまう事で、ソフトマージンSVMが実現できる。多くの文献では、スラック変数のノルムの取り方で異なる2種類のソフトマージンSVMの式を提示している:

1ノルムソフトマージンSVM・主問題

\begin{equation*} \begin{aligned} & \min_{\scriptsize \boldsymbol{w}} \frac{1}{2} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{w} + C_{1}\sum_{i=1}^{N} \eta_{i} \\ & \text{subject to : } y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i}) + b) \geq 1 - \eta_{i}, \ \eta_{i} \geq 0 \quad (i=1, \dots, N) \end{aligned} \end{equation*}

2ノルムソフトマージンSVM・主問題

\begin{equation*} \begin{aligned} &\min_{\scriptsize \boldsymbol{w}} \frac{1}{2} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{w} + \frac{C_{2}}{2}\sum_{i=1}^{N} \eta_{i}^{2} \quad \\ &\text{subject to : } y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i}) + b) \geq 1 - \eta_{i} \quad (i=1, \dots, N) \end{aligned} \end{equation*}

ここで、 \(C_{1}, C_{2}\)はハードマージンとソフトマージンのトレードオフを与える定数 [9] で、最適な値は実験等によって求める必要がある。双対問題の導出は、前節までの議論と同様に、 KKT条件に当てはめる事により得られる:

1ノルムソフトマージンSVM・双対問題の導出

ラグランジアンは、 \(\beta_{i} \geq 0\)なる双対変数を導入して、\(-\beta_{i}\eta_{i} \leq 0\)より、

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{w}, \boldsymbol{\eta}, \boldsymbol{\alpha}, \boldsymbol{\beta}) = \frac{1}{2} \boldsymbol{w}^{\mathsf{T}} \boldsymbol{w} + C_{1} \sum_{i=1}^{N}\eta_{i} + \sum_{i=1}^{N} \alpha_{i} \left\{ 1 - \eta_{i} - y_{i}(\boldsymbol{w}^{\mathsf{T}} \boldsymbol{\phi}(\boldsymbol{x}_{i}) + b) \right\} + \sum_{i=1}^{N}(-\beta_{i}\eta_{i}) \end{aligned} \end{equation*}

より、\({\cal L}(\boldsymbol{w}, \boldsymbol{\eta}, \boldsymbol{\alpha}, \boldsymbol{\beta})\)の\(\boldsymbol{w}, b, \eta_{i},\)による偏微分\(\displaystyle\frac{\partial \cal L}{\partial \boldsymbol{w}}, \frac{\partial \cal L}{\partial b}, \frac{\partial \cal L}{\partial \eta_{i}}\)は、

\begin{equation*} \begin{aligned} \frac{\partial \cal L}{\partial \boldsymbol{w}} = \boldsymbol{w} - \sum_{i=1}^{N} y_{i} \alpha_{i} \boldsymbol{\phi}(\boldsymbol{x}_{i}), \quad \frac{\partial \cal L}{\partial b} = \sum_{i=1}^{N}\alpha_{i}y_{i}, \quad \frac{\partial \cal L}{\partial \eta_{i}} = C_{1} - \alpha_{i} - \beta_{i} \end{aligned} \end{equation*}

\(\displaystyle\frac{\partial \cal L}{\partial \boldsymbol{w}} = \boldsymbol{0}, \frac{\partial \cal L}{\partial \eta_{i}} = 0\)とおくことで、最適時パラメタは、

\begin{equation*} \begin{aligned} \boldsymbol{w}^{\star} = \sum_{i=1}^{N} y_{i} \alpha_{i} \boldsymbol{\phi}(\boldsymbol{x}_{i}), \quad C_{1} = \alpha_{i} + \beta_{i} \end{aligned} \end{equation*}

\(\boldsymbol{w}^{\star}\)をラグランジアンに代入すると、

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\eta}^{\star}、 \boldsymbol{\alpha}、 \boldsymbol{\beta}) &= \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) + \sum_{i=1}^{N} (C_{1} - \alpha_{i} - \beta_{i}) \eta_{i} \\ &= \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \end{aligned} \end{equation*}

制約条件\(\alpha_{i}, \beta_{i} \geq 0\)を含めて考えると、\(\beta_{i} = C_{1} - \alpha_{i} \geq 0\)より、\(\alpha_{i}\)についての制約\(0 \leq \alpha_{i} \leq C_{1}\)が得られ、結局、普通のSVMの双対問題に\(\alpha_{i}\)についての制約を加えるだけで、1ノルムソフトマージンSVMが実現できる。

1ノルムソフトマージンSVM・双対問題

\begin{equation*} \begin{aligned} &\max_{\scriptsize \boldsymbol{\alpha}} \left[ \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \right] \\ &\text{subject to : } 0 \leq \alpha_{i} \leq C_{1}, \ \sum_{i=1}^{N} \alpha_{i}y_{i} = 0 \quad (i = 1, \dots, N) \nonumber\end{aligned} \end{equation*}

2ノルムソフトマージンSVM・双対問題の導出

ラグランジアンは、

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{w}, \boldsymbol{\eta}, \boldsymbol{\alpha}) = \frac{1}{2} \boldsymbol{w}^{\mathsf{T}} \boldsymbol{w} + \frac{C_{2}}{2} \sum_{i=1}^{N}\eta_{i}^{2} + \sum_{i=1}^{N} \alpha_{i} \left\{ 1 - \eta_{i} - y_{i}(\boldsymbol{w}^{\mathsf{T}} \boldsymbol{\phi}(\boldsymbol{x}_{i}) + b) \right\} \end{aligned} \end{equation*}

より、\({\cal L}(\boldsymbol{w}, \boldsymbol{\eta}, \boldsymbol{\alpha})\)の\(\boldsymbol{w}, b, \eta_{i}\)による偏微分\(\displaystyle\frac{\partial \cal L}{\partial \boldsymbol{w}}, \frac{\partial \cal L}{\partial b}, \frac{\partial \cal L}{\partial \eta_{i}}\)は、

\begin{equation*} \begin{aligned} \frac{\partial \cal L}{\partial \boldsymbol{w}} = \boldsymbol{w} - \sum_{i=1}^{N} y_{i} \alpha_{i} \boldsymbol{\phi}(\boldsymbol{x}_{i}), \quad \frac{\partial \cal L}{\partial b} = \sum_{i=1}^{N}\alpha_{i}y_{i}, \quad \frac{\partial \cal L}{\partial \eta_{i}} = C_{2}\eta_{i} - \alpha_{i} \end{aligned} \end{equation*}

\(\displaystyle\frac{\partial \cal L}{\partial \boldsymbol{w}} = \boldsymbol{0}, \frac{\partial \cal L}{\partial \eta_{i}} = 0\)とおくことで、最適時パラメタは、

\begin{equation*} \begin{aligned} \boldsymbol{w}^{\star} = \sum_{i=1}^{N} y_{i} \alpha_{i} \boldsymbol{\phi}(\boldsymbol{x}_{i}), \quad \eta_{i}^{\star} = \frac{\alpha_{i}}{C_{2}} \end{aligned} \end{equation*}

これをラグランジアンに代入すると、

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\eta}^{\star}, \boldsymbol{\alpha}) &= \sum_{i=1}^{N} \alpha_{i} + \frac{1}{2C_{2}} \sum_{i=1}^{N} \alpha_{i}^{2} + \sum_{i=1}^{N} \alpha_{i} \left[ - \frac{\alpha_{i}}{C_{2}} - y_{i} \sum_{j=1}^{N} y_{j}\alpha_{j} K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \right] + \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \\ &= \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2C_{2}} \sum_{i=1}^{N} \alpha_{i}^{2} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \end{aligned} \end{equation*}

ここで\(y_{i}y_{j} \in \{-1, 1\}\)に注目すれば、

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\eta}^{\star}, \boldsymbol{\alpha}) = \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\left( K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) + \frac{1}{C_{2}}\delta_{ij} \right) \end{aligned} \end{equation*}

と整理できる。ここで\(\delta_{ij}\)はディラックのデルタであり、

\begin{equation*} \begin{aligned} \delta_{ij} = \left\{ \begin{array}{ll} 1 & i = j \\ 0 & otherwise \end{array} \right. \end{aligned} \end{equation*}

を満たす。 2ノルムソフトマージンSVMも、結局、カーネル関数を簡単に書き換える事で実現できる。

2ノルムソフトマージンSVM・双対問題

\begin{equation*} \begin{aligned} &\max_{\scriptsize \boldsymbol{\alpha}} \left[ \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\left(K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) + \frac{1}{C_{2}}\delta_{ij} \right) \right] \\ &\text{subject to : } \alpha_{i} \geq 0, \ \sum_{i=1}^{N} \alpha_{i}y_{i} = 0 \quad (i = 1,\dots,N) \nonumber \end{aligned} \end{equation*}

SVR（Support Vector Regression, サポートベクトル回帰）

一般にSVMは識別器として用いられる事がほとんどだが、ラベルを実数とした回帰問題 [10] にも適用することができる。SVMによる回帰モデルのことを、 SVR（Support Vector Regression, サポートベクトル回帰）という。基本的な考え方としては、図の様に、識別面（回帰面）を中心に幅\(2\varepsilon\)の“帯”に多くのサンプルが入るようにすれば良い。

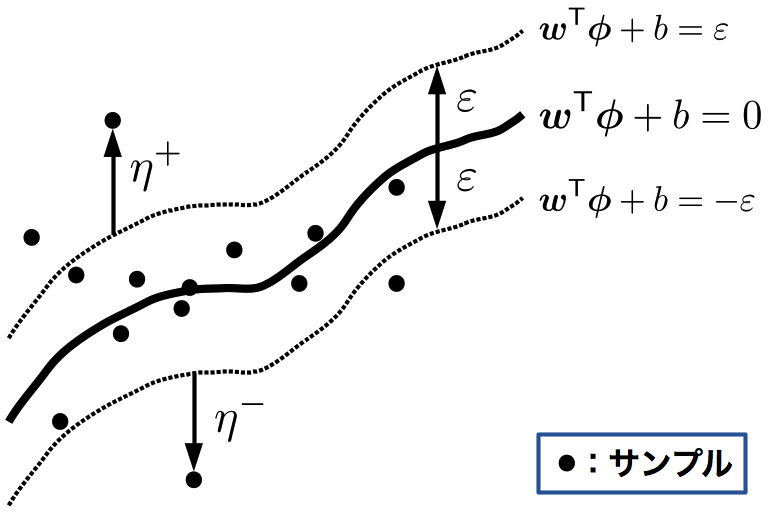
SVR

帯を考慮して制約を表現すると、

\begin{equation*} \begin{aligned} | y_{i} - (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i})+b) | \leq \varepsilon \quad (i = 1, \dots, N) \end{aligned} \end{equation*}

となる。これはハードマージン的な制約であり、幅\(2\varepsilon\)の帯に全てのサンプルが入る事を要求している。もちろん\(\varepsilon\)を十分に大きくとれば全てのサンプルは帯に入るが、帯が広すぎるために自由度が大きく、結果汎化性能の悪化に繋がってしまう。ラベルが実数となり、雑音の影響をより受けやすくなることから、SVRにおいては、最初からスラック変数を用いて、ソフトマージン的に定式化することが多い。

スラック変数を用いて、帯から飛び出た距離\(\eta_{i}^{+}, \eta_{i}^{-} \geq 0\)を次で定義する（図参照）:

\begin{align*} \begin{aligned} \eta_{i}^{+} = \left\{ \begin{array}{ll} y_{i} - \varepsilon - (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i})+b) & y_{i} \geq (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i})+b) + \varepsilon \\ 0 & otherwise \end{array} \right. \\ \eta_{i}^{-} = \left\{ \begin{array}{ll} (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i})+b) - y_{i} - \varepsilon & y_{i} \leq (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i})+b) - \varepsilon \\ 0 & otherwise \end{array} \right. \end{aligned} \end{align*}

なお、サンプルは帯からどちらか一方にしか飛び出ないので、\(\eta_{i}^{+}, \eta_{i}^{-}\)のいずれか一方は必ず\(0\)となり、サンプルが帯に収まっている時は両方共\(0\)となる。スラック変数を用いる事で、制約は次のように表現できる:

\begin{equation*} \begin{aligned} \left\{ \begin{array}{l} (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i})+b) - y_{i} \leq \varepsilon + \eta_{i}^{-} \\ y_{i} - (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{i})+b) \leq \varepsilon + \eta_{i}^{+} \end{array} \right. \end{aligned} \end{equation*}

ソフトマージンの時と同様に考える事で、最適化問題が定式化できる:

1ノルムSVR・主問題

\begin{equation*} \begin{aligned} &\min_{\scriptsize \boldsymbol{w}} \frac{1}{2} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{w} + C_{1}\sum_{i=1}^{N} (\eta_{i}^{+} + \eta_{i}^{-}) \\ &\text{subject to : } (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) - y_{i} \leq \varepsilon + \eta_{i}^{-}, \ y_{i} - (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) \leq \varepsilon + \eta_{i}^{+} \quad (i=1,\dots,N) \end{aligned} \end{equation*}

2ノルムSVR・主問題

\begin{equation*} \begin{aligned} &\min_{\scriptsize \boldsymbol{w}} \frac{1}{2} \boldsymbol{w}^{\mathsf{T}}\boldsymbol{w} + \frac{C_{2}}{2}\sum_{i=1}^{N} \left\{ (\eta_{i}^{+})^{2} + (\eta_{i}^{-})^{2} \right\} \\ &\text{subject to : } (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) - y_{i} \leq \varepsilon + \eta_{i}^{-}, \ y_{i} - (\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}_{i} + b) \leq \varepsilon + \eta_{i}^{+} \quad (i=1, \dots, N) \end{aligned} \end{equation*}

後はKKT条件にぶち込むだけの流れ作業である。よし、じゃあぶち込んでやるぜ！

1ノルムSVR・双対問題の導出

\begin{equation*} \begin{aligned} \begin{split} &{\cal L}(\boldsymbol{w}, \boldsymbol{\eta}^{+}, \boldsymbol{\eta}^{-}, \boldsymbol{\alpha}^{+}, \boldsymbol{\alpha}^{-}, \boldsymbol{\beta}^{+}, \boldsymbol{\beta}^{-}) = \\ &\frac{1}{2} \boldsymbol{w}^{\mathsf{T}} \boldsymbol{w} + C_{1} \sum_{i=1}^{N}(\eta_{i}^{+}+\eta_{i}^{-}) + \sum_{i=1}^{N}(-\beta_{i}^{+}\eta_{i}^{+} -\beta_{i}^{-}\eta_{i}^{-} ) \\ &+ \sum_{i=1}^{N} \left[ \alpha_{i}^{-} \left\{ (\boldsymbol{w}^{\mathsf{T}} \boldsymbol{\phi}(\boldsymbol{x}_{i}) + b) - y_{i} - \varepsilon - \eta_{i}^{-} \right\} + \alpha_{i}^{+} \left\{ y_{i} - (\boldsymbol{w}^{\mathsf{T}} \boldsymbol{\phi}(\boldsymbol{x}_{i}) + b) - \varepsilon - \eta_{i}^{+} \right\} \right] \end{split} \end{aligned} \end{equation*}

より、\({\cal L}(\boldsymbol{w}, \boldsymbol{\eta}^{+}, \boldsymbol{\eta}^{-}, \boldsymbol{\alpha}^{+}, \boldsymbol{\alpha}^{-}, \boldsymbol{\beta}^{+}, \boldsymbol{\beta}^{-})\)の\(\boldsymbol{w}, b, \eta_{i}^{+}, \eta_{i}^{-}\)による偏微分\(\displaystyle\frac{\partial \cal L}{\partial \boldsymbol{w}}, \frac{\partial \cal L}{\partial b}, \frac{\partial \cal L}{\partial \eta_{i}^{+}}, \frac{\partial \cal L}{\partial \eta_{i}^{-}}\)は、

\begin{equation*} \begin{aligned} \frac{\partial \cal L}{\partial \boldsymbol{w}} = \boldsymbol{w} + \sum_{i=1}^{N}(\alpha_{i}^{-} - \alpha_{i}^{+}) \boldsymbol{\phi}(\boldsymbol{x}_{i}), \quad \frac{\partial \cal L}{\partial b} = \sum_{i=1}^{N}(\alpha_{i}^{-} - \alpha_{i}^{+}) \\ \frac{\partial \cal L}{\partial \eta_{i}^{+}} = C_{1} - \alpha_{i}^{+} - \beta_{i}^{+}, \quad \frac{\partial \cal L}{\partial \eta_{i}^{-}} = C_{1} - \alpha_{i}^{-} - \beta_{i}^{-} \end{aligned} \end{equation*}

それぞれ\(0\)とおくと、

\begin{equation*} \begin{aligned} \boldsymbol{w}^{\star} = \sum_{i=1}^{N} (\alpha_{i}^{+} - \alpha_{i}^{-}) \boldsymbol{\phi}(\boldsymbol{x}_{i}), \quad \sum_{i=1}^{N}(\alpha_{i}^{-} - \alpha_{i}^{+}) = 0, \quad C_{1} = \alpha_{i}^{+} + \beta_{i}^{+} = \alpha_{i}^{-} + \beta_{i}^{-} \end{aligned} \end{equation*}

これをラグランジアンに代入すると、

\begin{equation*} \begin{aligned} \begin{split} &{\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\eta}^{+\star}, \boldsymbol{\eta}^{-\star}, \boldsymbol{\alpha}^{+}, \boldsymbol{\alpha}^{-}, \boldsymbol{\beta}^{+}, \boldsymbol{\beta}^{-}) = \\ &\frac{1}{2} \sum_{i、j=1}^{N} (\alpha_{i}^{+} - \alpha_{i}^{-})(\alpha_{j}^{+} - \alpha_{j}^{-})K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) + C_{1} \sum_{i=1}^{N}(\eta_{i}^{+}+\eta_{i}^{-}) - \sum_{i=1}^{N}(\beta_{i}^{+}\eta_{i}^{+} + \beta_{i}^{-}\eta_{i}^{-}) \\ &+\sum_{i=1}^{N} \left[ \alpha_{i}^{-}\sum_{j=1}^{N}(\alpha_{j}^{+}-\alpha_{j}^{-})K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) - \alpha_{i}^{+}\sum_{j=1}^{N}(\alpha_{j}^{+}-\alpha_{j}^{-})K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \right] \\ &+\sum_{i=1}^{N}\left[ \alpha_{i}^{-} (-\varepsilon-\eta_{i}^{-}-y_{i}) + \alpha_{i}^{+} (-\varepsilon-\eta_{i}^{+}+y_{i}) \right] \end{split} \end{aligned} \end{equation*}

\(C_{1} = \alpha_{i}^{+} + \beta_{i}^{+} = \alpha_{i}^{-} + \beta_{i}^{-}\)を用いて整理すると、

\begin{equation*} \begin{aligned} \begin{split} &{\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\eta}^{+\star}, \boldsymbol{\eta}^{-\star}, \boldsymbol{\alpha}^{+}, \boldsymbol{\alpha}^{-}, \boldsymbol{\beta}^{+}, \boldsymbol{\beta}^{-}) = \\ &\sum_{i=1}^{N}(\alpha_{i}^{+}-\alpha_{i}^{-}) - \varepsilon\sum_{i=1}^{N}(\alpha_{i}^{-}+\alpha_{i}^{+}) - \frac{1}{2} \sum_{i、j=1}^{N} (\alpha_{i}^{+} - \alpha_{i}^{-})(\alpha_{j}^{+} - \alpha_{j}^{-})K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \end{split} \end{aligned} \end{equation*}

ところで、上でも既に述べたが\(\eta_{i}^{+}, \eta_{i}^{-}\)のどちらか一方は必ず\(0\)となるので、その場合は対応する\(\alpha_{i}^{+}, \alpha_{i}^{-}\)の制約条件はなくなり、従って、 \(\alpha_{i}^{+}, \alpha_{i}^{-}\)のどちらか一方も\(0\)となる。この事から\(\alpha_{i} = \alpha_{i}^{+} - \alpha_{i}^{-}\)とおけば、\(\alpha_{i}^{-} + \alpha_{i}^{+} = |\alpha_{i}|\)と表現できるので、双対問題は以下の様に表現できる。

1ノルムSVR・双対問題

\begin{equation*} \begin{aligned} &\max_{\scriptsize \boldsymbol{\alpha}} \left[ \sum_{i=1}^{N}y_{i}\alpha_{i} - \varepsilon\sum_{i=1}^{N}|\alpha_{i}| - \frac{1}{2} \sum_{i、j=1}^{N}\alpha_{i}\alpha_{j}K(\boldsymbol{x}_{i}、 \boldsymbol{x}_{j}) \right] \\ &\text{subject to : } \sum_{i=1}^{N}\alpha_{i} = 0, \ -C_{1} \leq \alpha_{i} \leq C_{1} \quad (i = 1、\dots、N) \nonumber \end{aligned} \end{equation*}

2ノルムSVR・双対問題の導出

\begin{equation*} \begin{aligned} &{\cal L}(\boldsymbol{w}, \boldsymbol{\eta}^{+}, \boldsymbol{\eta}^{-}, \boldsymbol{\alpha}^{+}, \boldsymbol{\alpha}^{-}) = \\ &\frac{1}{2} \boldsymbol{w}^{\mathsf{T}} \boldsymbol{w} + \frac{C_{2}}{2} \sum_{i=1}^{N} \{ (\eta_{i}^{+})^{2} + (\eta_{i}^{-})^{2} \} \\ &+\sum_{i=1}^{N} \left[ \alpha_{i}^{-} \left\{ (\boldsymbol{w}^{\mathsf{T}} \boldsymbol{\phi}(\boldsymbol{x}_{i}) + b) - y_{i} - \varepsilon - \eta_{i}^{-} \right\} + \alpha_{i}^{+} \left\{ y_{i} - (\boldsymbol{w}^{\mathsf{T}} \boldsymbol{\phi}(\boldsymbol{x}_{i}) + b) - \varepsilon - \eta_{i}^{+} \right\} \right] \end{aligned} \end{equation*}

より、\({\cal L}(\boldsymbol{w}, \boldsymbol{\eta}^{+}, \boldsymbol{\eta}^{-}, \boldsymbol{\alpha}^{+}, \boldsymbol{\alpha}^{-})\)の\(\boldsymbol{w}, b, \eta_{i}^{+}, \eta_{i}^{-}\)による偏微分\(\displaystyle\frac{\partial \cal L}{\partial \boldsymbol{w}}, \frac{\partial \cal L}{\partial b}, \frac{\partial \cal L}{\partial \eta_{i}^{+}}, \frac{\partial \cal L}{\partial \eta_{i}^{-}}\)は、

\begin{equation*} \begin{aligned} \frac{\partial \cal L}{\partial \boldsymbol{w}} = \boldsymbol{w} + \sum_{i=1}^{N}(\alpha_{i}^{-} - \alpha_{i}^{+}) \boldsymbol{\phi}(\boldsymbol{x}_{i}), \quad \frac{\partial \cal L}{\partial b} = \sum_{i=1}^{N}(\alpha_{i}^{-} - \alpha_{i}^{+}) \\ \frac{\partial \cal L}{\partial \eta_{i}^{+}} = C_{2}\eta_{i}^{+} - \alpha_{i}^{+}, \quad \frac{\partial \cal L}{\partial \eta_{i}^{-}} = C_{2}\eta_{i}^{-} - \alpha_{i}^{-} \end{aligned} \end{equation*}

それぞれ\(0\)とおくと、

\begin{equation*} \begin{aligned} \boldsymbol{w}^{\star} = \sum_{i=1}^{N} (\alpha_{i}^{+} - \alpha_{i}^{-}) \boldsymbol{\phi}(\boldsymbol{x}_{i}), \quad \sum_{i=1}^{N}(\alpha_{i}^{-} - \alpha_{i}^{+}) = 0, \quad \eta_{i}^{+\star} = \frac{\alpha_{i}^{+}}{C_{2}}, \quad \eta_{i}^{-\star} = \frac{\alpha_{i}^{-}}{C_{2}} \end{aligned} \end{equation*}

\(\boldsymbol{w}^{\star}\)をラグランジアンに代入すると、

\begin{equation*} \begin{aligned} \begin{split} &{\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\eta}^{+\star}, \boldsymbol{\eta}^{-\star}, \boldsymbol{\alpha}^{+},\boldsymbol{\alpha}^{-}) = \\ &\frac{1}{2} \sum_{i、j=1}^{N} (\alpha_{i}^{+} - \alpha_{i}^{-})(\alpha_{j}^{+} - \alpha_{j}^{-})K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) + \frac{1}{C_{2}} \sum_{i=1}^{N}\left\{ (\alpha_{i}^{+})^{2}+(\alpha_{i}^{-})^{2} \right\} \\ &+\sum_{i=1}^{N} \left[ \alpha_{i}^{-}\sum_{j=1}^{N}(\alpha_{j}^{+}-\alpha_{j}^{-})K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) - \alpha_{i}^{+}\sum_{j=1}^{N}(\alpha_{j}^{+}-\alpha_{j}^{-})K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \right] \\ &+\sum_{i=1}^{N}\left[ \alpha_{i}^{-} (-\varepsilon - \frac{\alpha_{i}^{-}}{C_{2}} - y_{i}) + \alpha_{i}^{+} (- \varepsilon - \frac{\alpha_{i}^{+}}{C_{2}} +y_{i}) \right] \\ &=\sum_{i=1}^{N} (\alpha_{i}^{+} - \alpha_{i}^{-})y_{i} - \frac{1}{2} \sum_{i、j=1}^{N}(\alpha_{i}^{+}-\alpha_{i}^{-})(\alpha_{j}^{+}-\alpha_{j}^{-})K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) \\ &-\varepsilon\sum_{i=1}^{N}(\alpha_{i}^{-} + \alpha_{i}^{+}) - \frac{1}{2C_{2}}\sum_{i=1}^{N}\left\{ (\alpha_{i}^{-})^{2} + (\alpha_{i}^{+})^{2} \right\} \end{split} \end{aligned} \end{equation*}

1ノルムSVRの時と同様に、\(\alpha_{i} = \alpha_{i}^{+} - \alpha_{i}^{-}\)とおくと、\((\alpha_{i}^{+})^{2} + (\alpha_{i}^{-})^{2} = \alpha_{i}^{2}\)が成り立つので、双対問題は以下の様に表現できる。

2ノルムSVR・双対問題

\begin{equation*} \begin{aligned} & \max_{\scriptsize \boldsymbol{\alpha}} \left[ \sum_{i=1}^{N}y_{i}\alpha_{i} - \varepsilon\sum_{i=1}^{N}|\alpha_{i}| - \frac{1}{2} \sum_{i, j=1}^{N}\alpha_{i}\alpha_{j}\left( K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) + \frac{1}{C_{2}} \right) \right] \\ & \text{subject to : } \sum_{i=1}^{N}\alpha_{i} = 0 \quad (i = 1, \dots, N) \nonumber \end{aligned} \end{equation*}

実装の例

実装例はここにある。本稿では要点を絞って見ていく。

学習

学習則の導出

SVMの学習は、双対問題

\begin{equation*} \begin{aligned} &\max_{\scriptsize \boldsymbol{\alpha}} \left[ \sum_{i=1}^{N} \alpha_{i} - \frac{1}{2} \sum_{i、j=1}^{N} \alpha_{i}\alpha_{j}y_{i}y_{j}\boldsymbol{\phi}(\boldsymbol{x}_{i})^{\mathsf{T}}\boldsymbol{\phi}(\boldsymbol{x}_{j}) \right] = \max_{\scriptsize \boldsymbol{\alpha}} {\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\alpha}) \\ &\text{subject to : } \alpha_{i} \geq 0,\ \sum_{i=1}^{N} \alpha_{i}y_{i} = 0 \quad (i = 1, \dots, N) \end{aligned} \end{equation*}

を解けば良いことになる。脚注 [11] で既に触れたが、SVMのマージン最大化は凸計画問題である。従って局所最適解が存在せず、極大値が大域的な最大値に一致する。ソフトマージンに対応する時は、1ノルムソフトマージンの際には係数に値域\(0 \geq \alpha_{i} \geq C_{1}\ (i=1,...,N)\)を設け、2ノルムの際にはカーネル関数\(K\)を次のように書き換えれば良い：

\begin{equation*} K'(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) = K(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}) + \frac{\delta_{ij}}{C_{2}} \end{equation*}

ここでは簡単な最急勾配法によって解を求めることを考える。最急勾配法の原理は単純である。\(F(\boldsymbol{\alpha}) = {\cal L}(\boldsymbol{w}^{\star}, \boldsymbol{\alpha})\) とおくと、その\(\boldsymbol{\alpha}\)による偏微分\(\frac{\partial F(\boldsymbol{\alpha})}{\partial \boldsymbol{\alpha}}\)は勾配、即ち\(F(\boldsymbol{\alpha})\)の最も上昇する方向を指すベクトルとなるので、係数の更新量\(\Delta\boldsymbol{\alpha}\)は学習率\(\eta > 0\)を用いて

\begin{equation*} \Delta \boldsymbol{\alpha} = \eta \frac{\partial F(\boldsymbol{\alpha})}{\partial \boldsymbol{\alpha}} \end{equation*}

とすれば良い [12] 。学習の収束判定は、例えば\(||\Delta \boldsymbol{\alpha}||\)が十分小さくなった時とすれば良く、その時は極大値が得られている。実際に\(\frac{\partial F(\boldsymbol{\alpha})}{\partial \boldsymbol{\alpha}}\)を計算することを考える。\(\frac{\partial F(\boldsymbol{\alpha})}{\partial \alpha_{i}}\ (i=1,...,N)\)は、

\begin{equation*} \begin{aligned} \frac{\partial F(\boldsymbol{\alpha})}{\partial \alpha_{i}} &= 1 - \frac{1}{2} \frac{\partial}{\partial \alpha_{i}} \left( \alpha_{1} \alpha_{1} y_{1} y_{1} \boldsymbol{x}_{1}^{\mathsf{T}} \boldsymbol{x}_{1} + ... + \alpha_{i} \alpha_{1} y_{i} y_{1} \boldsymbol{x}_{i}^{\mathsf{T}} \boldsymbol{x}_{1} + ... + \alpha_{i} \alpha_{N} y_{i} y_{N} \boldsymbol{x}_{i}^{\mathsf{T}} \boldsymbol{x}_{N} + ... + \alpha_{1} \alpha_{i} y_{1} y_{i} \boldsymbol{x}_{1}^{\mathsf{T}} \boldsymbol{x}_{i} + ... + \alpha_{N} \alpha_{i} y_{N} y_{i} \boldsymbol{x}_{N}^{\mathsf{T}} \boldsymbol{x}_{i} + ... + \alpha_{N} \alpha_{N} y_{N} y_{N} \boldsymbol{x}_{N}^{\mathsf{T}} \boldsymbol{x}_{N} \right) \\ &= 1 - \sum_{j=1}^{N} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\mathsf{T}} \boldsymbol{x}_{j} \end{aligned} \end{equation*}

よって、ステップ\(t\)時の係数\(\alpha_{i}(t)\ (i=1,...,N)\)について以下の更新規則に従って学習を行えば良い：

\begin{equation*} \alpha_{i}(t+1) = \alpha_{i}(t) + \eta \left( 1 - \sum_{j=1}^{N} \alpha_{j} y_{i} y_{j} \boldsymbol{x}_{i}^{\mathsf{T}} \boldsymbol{x}_{j} \right) \end{equation*}

実装

学習を行っている箇所を抜粋すると次の様になる：

/* 勾配値の計算 */
diff_dist = 0.0f;
for (i_x = 0; i_x < handle->sample_num; ++i_x) {
  diff_sum = 0.0f;
  for (i_y = 0; i_y < handle->sample_num; ++i_y) {
    /* C2を踏まえたカーネル関数値を計算 */
    kernel_val = GRAM_MATRIX_AT(handle->gram_matrix, handle->sample_num, i_x, i_y);
    if (i_x == i_y) {
      kernel_val += (1.0f / soft_margin_C2);
    }
    diff_sum += handle->dual_coef[i_y] * handle->sample_label[i_y] * kernel_val;
  }
  diff_sum *= handle->sample_label[i_x];
  diff_dual_coef[i_x] = 1.0f - diff_sum;
  diff_dist += (1.0f - diff_sum) * (1.0f - diff_sum);
}

/* 双対係数の更新 */
for (i_sample = 0; i_sample < handle->sample_num; ++i_sample) {
  if ( handle->sample_label[i_sample] == 0 ) {
    continue;
  }
  /* printf("dual_coef[%d]:%f -> ", i_sample, handle->dual_coef[i_sample]); */
  handle->dual_coef[i_sample]
    += handle->learning_rate * (diff_dual_coef[i_sample] + SMPSVM_MOMENT_RATE * pre_diff_dual_coef[i_sample]);
  /* printf("%f \n", handle->dual_coef[i_sample]); */

  /* 非数,無限チェック */
  if ( isnan(handle->dual_coef[i_sample]) || isinf(handle->dual_coef[i_sample]) ) {
    fprintf(stderr, "Detected NaN or Inf Dual-Coffience. \n");
    return -3;
  }
}

既にコメントが付いているが、特筆すべき点について補足する。

/* C2を踏まえたカーネル関数値を計算 */
kernel_val = GRAM_MATRIX_AT(handle->gram_matrix, handle->sample_num, i_x, i_y);

予め計算しておいたカーネル関数値をグラム行列から取り出している。学習中は何度もカーネル関数値を計算するため、グラム行列を用意しておくことで若干高速化できる。

if (i_x == i_y) {
  kernel_val += (1.0f / soft_margin_C2);
}

2ノルムソフトマージンのカーネル関数値を加味している。2ノルムソフトマージンを使用しない場合はsoft_margin_C2 == FLT_MAXとなっているため、無視できる。

handle->dual_coef[i_sample]
  += handle->learning_rate * (diff_dual_coef[i_sample] + SMPSVM_MOMENT_RATE * pre_diff_dual_coef[i_sample]);

係数更新を行っている。ここでは、単純な最急勾配分のみだけではなく、前回の勾配値に定数を乗じて加えたモーメント法を使用している。一般にモーメント法を使用したほうが学習が早くなることが知られている。

制約条件の考慮

学習則は単純に見えても実装時に落とし穴になるのが制約条件である。

正例と負例の双対係数の和を等しくする

KKT条件から導かれる\(\boldsymbol{\alpha}\)についての制約

\begin{equation*} \sum_{i=1}^{N} \alpha_{i}y_{i} = 0 \end{equation*}

を実現するのが案外難しい。上の制約から、

\begin{equation*} \begin{aligned} &\sum_{y_{i}=1} \alpha_{i} - \sum_{y_{i}=-1} \alpha_{i} = 0 \\ &\iff \sum_{y_{i}=1} \alpha_{i} = \sum_{y_{i}=-1} \alpha_{i} \end{aligned} \end{equation*}

が導かれるため、正例と負例の双対係数の和は等しくなる事が分かる。本実装では、\(\alpha_{i}y_{i}\)の平均を取り、全係数\(\alpha_{i}\ (i=1,...,N)\)をその平均に寄せることで上記の制約を満たすように係数を修正している。

/* 制約1: 正例と負例の双対係数和を等しくする. */
dual_coef_average = 0.0f;
for (i_sample = 0; i_sample < handle->sample_num; ++i_sample) {
  dual_coef_average
    += (handle->sample_label[i_sample] * handle->dual_coef[i_sample]);
}
dual_coef_average /= handle->sample_num;
for (i_sample = 0; i_sample < handle->sample_num; ++i_sample) {
  if ( handle->sample_label[i_sample] == 0 ) {
    continue;
  }
  handle->dual_coef[i_sample]
    -= (dual_coef_average / handle->sample_label[i_sample]);
}

この制約を満たすための実装はこの限りではない。

双対係数は非負

双対係数は非負でなければならないため、負になった係数は全て0に修正してしまう。学習が進むに連れて0の係数が増えていくが、それはSVMの持つスパース学習の効果が現れている状態である。学習が収束した時、0に潰れず非負値となった係数に対応するサンプルがサポートベクトルである。

/* 制約2: 双対係数は非負 */
coef_dist = 0.0f;
for (i_sample = 0; i_sample < handle->sample_num; ++i_sample) {
  if ( handle->dual_coef[i_sample] < 0.0f ) {
    handle->dual_coef[i_sample] = 0.0f;
  } else if ( handle->dual_coef[i_sample] > soft_margin_C1 ) {
    /* C1ノルムの制約を適用 */
    handle->dual_coef[i_sample] = soft_margin_C1;
  }
  /* ここで最終結果が出る. 前回との変化を計算 */
  coef_diff = pre_dual_coef[i_sample] - handle->dual_coef[i_sample];
  coef_dist += (coef_diff * coef_diff);
}

本実装では、非負条件に咥えて1ノルムソフトマージンの制約も追加で判定している。1ノルムソフトマージンを使用しない時はsoft_margin_C1 == FLT_MAXとなっているため、無視できる。

識別

マージンの定式化で述べたが、SVMのクラス識別は出力値\(y\)の正負によって判断する [13] 。SVMの出力式

\begin{equation*} g(\boldsymbol{x}, \boldsymbol{w}) = \boldsymbol{w}^{\mathsf{T}} \boldsymbol{x} + b \end{equation*}

に、KKT条件における最適条件\(\boldsymbol{w}^{\star} = \sum_{i=1}^{N} \alpha_{i}y_{i}\boldsymbol{x}_{i}\)を代入すれば、次の双対表現が得られる：

\begin{equation*} g(\boldsymbol{x}, \boldsymbol{w}^{\star}) = \sum_{i=1}^{N} \alpha_{i} y_{i} K(\boldsymbol{x}_{i}, \boldsymbol{x}) + b \end{equation*}

識別の際には、学習済みの係数\(\boldsymbol{\alpha}\)を使用して上式を計算し、その正負を判定すれば良い。実装としては次の様になる：

/* ネットワーク出力計算 */
network_output = 0.0f;
for (i_sample = 0; i_sample < handle->sample_num; ++i_sample) {
  /* 係数が正に相当するサンプル（サポートベクトル）
   * のみを計算する */
  if (handle->dual_coef[i_sample] > 0.0f) {
    network_output
      += handle->sample_label[i_sample] * handle->dual_coef[i_sample]
      * handle->kernel_function(handle->sample_data[i_sample], normalized_data, data_dim, handle->kernel_parameter);
  }
}

/* 識別 */
*result = (network_output >= 0.0f) ? 1 : -1;

脚注

[1]	高村大也、奥村学、 “言語処理のための機械学習入門”、コロナ社、 2010

[2]	高橋治久、堀田一弘、 “学習理論” コロナ社、 2009

[3]	くどいかもしれないが、サポートベクトルは最も識別面に近いサンプルなので、この仮定により\(y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}+b) \geq l \quad (i=1, \dots, N)\)が成り立つ。

[4]

（証明） - 最適化対象について、\(\displaystyle \frac{1}{2}\boldsymbol{w}^{\mathsf{T}}\boldsymbol{w} = \frac{1}{2} \sum_{i=1}^{n} w_{i}^{2}\)より（\(\boldsymbol{w}=[w_{1}\dots w_{n}]^\mathsf{T}\)）、明らかに下に凸である。 - 制約条件について、\(W_{i} = \{ \boldsymbol{w} | y_{i}(\boldsymbol{w}^{\mathsf{T}}\boldsymbol{x}\_{i}+b) \geq 1 \}\)とおくと、\(\forall \boldsymbol{w}^{\prime}, \boldsymbol{w}^{\prime\prime} \in W_{i}, \forall t \in [0, 1]\)に対して、

\begin{equation*} \begin{aligned} y_{i} \left[ \left( t\boldsymbol{w}^{\prime\mathsf{T}} + (1-t) \boldsymbol{w}^{\prime\prime\mathsf{T}} \right) \boldsymbol{x}\_{i} + b \right] = y_{i} \left[ t(\boldsymbol{w}^{\prime\mathsf{T}}\boldsymbol{x}\_{i} - \boldsymbol{w}^{\prime\prime\mathsf{T}}\boldsymbol{x}\_{i}) + \boldsymbol{w}^{\prime\prime\mathsf{T}}\boldsymbol{x}\_{i} + b \right] \\ = y_{i} \left[ t\left( (\boldsymbol{w}^{\prime\mathsf{T}}\boldsymbol{x}\_{i} + b) - (\boldsymbol{w}^{\prime\prime\mathsf{T}}\boldsymbol{x}\_{i} + b) \right) + \boldsymbol{w}^{\prime\prime\mathsf{T}}\boldsymbol{x}\_{i} + b \right] \\ = t y_{i} (\boldsymbol{w}^{\prime\mathsf{T}}\boldsymbol{x}\_{i} + b) + (1-t) y_{i}(\boldsymbol{w}^{\prime\prime\mathsf{T}}\boldsymbol{x}\_{i} + b) \\ \geq t + (1-t) = 1\end{aligned} \end{equation*}

よって、\(t\boldsymbol{w}^{\prime} + (1-t) \boldsymbol{w}^{\prime\prime} \in W_{i}\)より\(W_{i}\)は凸集合。最適化問題においては、 \(W_{i}\)の共通部分\(\bigcap_{i=1}^{N} W_{i}\)を考えれば良く、 凸集合の積集合もまた凸集合 なので、制約条件も凸集合となる。以上の2点より、マージン最大化は凸計画問題。（凸集合の積集合もまた凸集合であることの証明）2つの凸集合を\(A_{1},A_{2}\)とする。両者の集合の積\(A_{1}\cap A_{2}\)が空集合ならば、空集合は凸集合と定義されるので命題は成立する。一般に\(A_{1}\cap A_{2}\)から2点\(x,y\)をとると, \(x, y\)を結ぶ線分は、 \(A_{1}, A_{2}\)は共に凸集合なので、 \(A_{1}\)にも\(A_{2}\)にも属していて飛び出ることはない。これは集合の積\(A_{1}\cap A_{2}\)が凸集合であることを示している。

[5]

（鞍点\((\boldsymbol{v}^{\star}, \boldsymbol{\alpha}^{\star})\)が最適点となる事の証明） \((\boldsymbol{v}^{\star}, \boldsymbol{\alpha}^{\star})\)は鞍点なので、

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{v}, \boldsymbol{\alpha}^{\star}) \leq {\cal L}(\boldsymbol{v}^{\star}, \boldsymbol{\alpha}^{\star}) \leq {\cal L}(\boldsymbol{v}^{\star}, \boldsymbol{\alpha}) \end{aligned} \end{equation*}

を満たす。従って右側の不等式から\(\boldsymbol{\alpha}^{\star\mathsf{T}}\boldsymbol{g}(\boldsymbol{v}^{\star}) \leq \boldsymbol{\alpha}^{\mathsf{T}}\boldsymbol{g}(\boldsymbol{v}^{\star})\)が任意の\(\boldsymbol{\alpha}\)で成立する。即ち\(\boldsymbol{\alpha} = \boldsymbol{0}\)の時、 \(g_{i}(\boldsymbol{v}^{\star}) \geq 0\)と併せて\(\boldsymbol{\alpha}^{\star\mathsf{T}}\boldsymbol{g}(\boldsymbol{v}^{\star}) = 0\)が成立する。更に、ここで関係式

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{v}, \boldsymbol{\alpha}^{\star}) - {\cal L}(\boldsymbol{v}^{\star}, \boldsymbol{\alpha}^{\star}) \leq \left( \frac{\partial {\cal L}(\boldsymbol{v}^{\star}, \boldsymbol{\alpha})}{\partial \boldsymbol{v}} \right)^{\mathsf{T}} (\boldsymbol{v} - \boldsymbol{v}^{\star}) \end{aligned} \end{equation*}

を用いる（証明は後術）と、鞍点であることから\(\displaystyle\frac{\partial {\cal L}(\boldsymbol{v}^{\star}, \boldsymbol{\alpha})}{\partial \boldsymbol{v}} = \boldsymbol{0}\)であり、また、 \(\boldsymbol{\alpha}^{\star\mathsf{T}}\boldsymbol{g}(\boldsymbol{v}^{\star}) = 0\)より、

\begin{equation*} \begin{aligned} {\cal L}(\boldsymbol{v}, \boldsymbol{\alpha}^{\star}) - {\cal L}(\boldsymbol{v}^{\star}, \boldsymbol{\alpha}^{\star}) &= {\cal L}(\boldsymbol{v}, \boldsymbol{\alpha}^{\star}) - f(\boldsymbol{v}^{\star}) \leq 0 \iff f(\boldsymbol{v}^{\star}) \geq {\cal L}(\boldsymbol{v}, \boldsymbol{\alpha}^{\star}) \end{aligned} \end{equation*}

が成り立つ。更に、もとより\(\boldsymbol{\alpha}^{\star\mathsf{T}}\boldsymbol{g}(\boldsymbol{v}) \geq 0\)なので、

\begin{equation*} \begin{aligned} f(\boldsymbol{v}) \leq f(\boldsymbol{v}) + \boldsymbol{\alpha}^{\star\mathsf{T}}\boldsymbol{g}(\boldsymbol{v}) = {\cal L}(\boldsymbol{v}, \boldsymbol{\alpha}^{\star}) \end{aligned} \end{equation*}

従って\(f(\boldsymbol{v}^{\star}) \geq f(\boldsymbol{v})\)が任意の\(\boldsymbol{v}\)で成立し、\((\boldsymbol{v}^{\star}, \boldsymbol{\alpha}^{\star})\)が最適点となる事が示された。次いで(＊)を証明する。\({\cal L}(\boldsymbol{v}, \boldsymbol{\alpha})\)が凸関数ならば、 \({\cal L}(t\boldsymbol{v}^{\prime}+(1-t)\boldsymbol{v}^{\prime\prime}, \boldsymbol{\alpha}^{\star}) \geq t {\cal L}(\boldsymbol{v}^{\prime}, \boldsymbol{\alpha}^{\star}) + (1-t) {\cal L}(\boldsymbol{v}^{\prime}, \boldsymbol{\alpha}^{\star})\)が\(t \in [0,1]\)で成立する。よって、

\begin{equation*} t{\cal L}(\boldsymbol{v}^{\prime}, \boldsymbol{\alpha}^{\star}) \leq t{\cal L}(\boldsymbol{v}^{\prime\prime}, \boldsymbol{\alpha}^{\star}) - {\cal L}(\boldsymbol{v}^{\prime\prime}, \boldsymbol{\alpha}^{\star}) + {\cal L}(t\boldsymbol{v}^{\prime}+(1-t)\boldsymbol{v}^{\prime\prime}, \boldsymbol{\alpha}^{\star}) \iff {\cal L}(\boldsymbol{v}^{\prime}, \boldsymbol{\alpha}^{\star}) \leq {\cal L}(\boldsymbol{v}^{\prime\prime}, \boldsymbol{\alpha}^{\star}) + \frac{{\cal L}(\boldsymbol{v}^{\prime\prime} + t(\boldsymbol{v}^{\prime}-\boldsymbol{v}^{\prime\prime}), \boldsymbol{\alpha}^{\star}) - {\cal L}(\boldsymbol{v}^{\prime\prime}, \boldsymbol{\alpha}^{\star})}{t} \end{equation*}

ここで\(t \to 0\)ならしめれば、方向微分と勾配の関係式より、

\begin{equation*} {\cal L}(\boldsymbol{v}^{\prime}, \boldsymbol{\alpha}^{\star}) - {\cal L}(\boldsymbol{v}^{\prime\prime}, \boldsymbol{\alpha}^{\star}) \leq \left( \frac{\partial {\cal L}(\boldsymbol{v}^{\prime\prime}, \boldsymbol{\alpha}^{\star})}{\partial \boldsymbol{v}} \right)^{\mathsf{T}} (\boldsymbol{v}^{\prime} - \boldsymbol{v}^{\prime\prime}) \end{equation*}

を得る。

[6]	互いに同一平面上以外の位置にある事。例えば、2次元空間では同一直線上以外の位置であり、3次元空間では同一平面上以外の位置である。異なるクラスのサンプルが一般位置にあれば、もとより線形分離可能である。

[7]

有限個数\(N<\infty\)のサンプルに対し、\((\boldsymbol{G})\_{ij} = K(\boldsymbol{x}\_{i}, \boldsymbol{x}\_{j})\)、即ち\((i,j)\)成分の値が\(K(\boldsymbol{x}\_{i}, \boldsymbol{x}\_{j})\)となっている行列\(\boldsymbol{G}\)をグラム（カーネル）行列という。特徴写像が有限次元ならば、グラム行列が（有限）正定値行列ならば\(K\)はカーネル関数となる。特徴写像が無限次元の場合のカーネル関数の条件がマーサーの定理である。その内容は、入力空間\(X\subset \mathbb{R}^{n}\)が有界閉集合（\(\iff\)コンパクト）であるとし、対象な連続関数\(K\)が正定値、即ち任意の二乗可積分（二乗積分可能）な関数\(f\)に対し

\begin{equation*} \begin{aligned} \int_{X\times X}K(x, z)f(x)f(z)dxdz \geq 0\end{aligned} \end{equation*}

ならば、ヒルベルト空間の正規直交基底\(\phi_{j}\ (j=1, 2, \dots)\)で次式が一様収束するものが存在する場合、\(K\)はカーネル関数である。

\begin{equation*} \begin{aligned} K(x, z) = \sum_{j=1}^{\infty} \phi_{j}(x)\phi_{j}(z) \end{aligned} \end{equation*}

[8]	サンプルに現れない未知のデータでももれなく識別できる能力

[9]	双対問題において、 \(C_{1}, C_{2} \to \infty\)とすると、ハードマージンSVMに一致することが分かる

[10]	サンプルに最も当てはまる曲線（面）を探す問題。もう少し形式的に言うと、各サンプル\(\boldsymbol{x}\_{i}\)でのラベル\(y_{i}\)の平均値を表す関数\(f\)を学習する問題。

[11]

[12]	ただし学習率\(\eta\)の決め方は問題依存である。一般に、\(\eta\)が小さすぎると学習が進行せず、大きすぎると極値を飛び越えてしまい学習が収束しない。

[13]	\(y = 0\)の場合の判断を明確にしている書類がない。ここでは正と判定する。

Related Posts: