LPCの多段構成検証(1)

迷ったけど性能が高いし研究室のテーマに合致するのでテーマを変えるのがいいと思った。

今やっているLPCの多段構成はResNetとの類似が指摘できる。F(x)がLPCの予測（に負号をとったもの）で、xと足すと残差が出力される。そして見ている区間を変えるのはストライド付きの畳み込みだ。

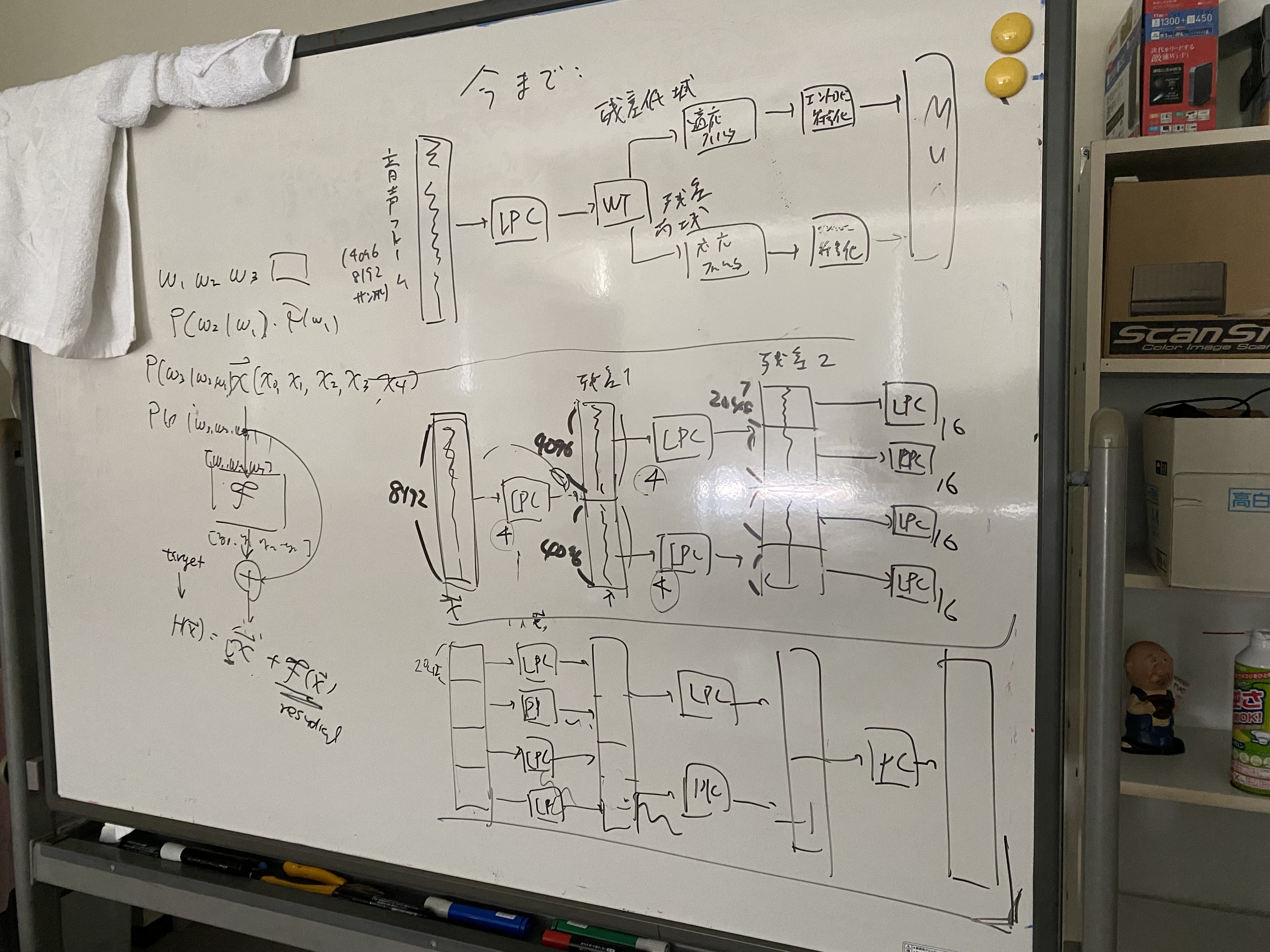
これがすごいのが学習できるということ。最終層でL1ノルムとかエントロピーを損失に設定して微分してバックプロパゲーション学習する。何なら最小二乗誤差で学習してもいい。LPCは層ごとに学習している（制約ボルツマシンの単層学習に相当？）からより良い解が見つかる可能性がある。

この構成は単純なLPCの組み合わせに過ぎないが性能がよい。時間がかかるのは学習（エンコード）のときだけだ。 しかし、まだ整理できてないし既存研究があるかどうかも不定。学習は詰めて定式化しなければなるまい。

ひとまず試すべきなのは、細かい分割から始めて荒くしていく方針はどうかというところ。以前試したが圧縮性能は良くなかった。今一度試してみる。

最小分割単位を2048, 最大ブロックサイズを(2048*8)として、LPCの次数はすべて4とする。

ワン・ツー・スゥイーツでは、

• (2048*8, 2048*4, 2048*2, 2048) の構成: 74.83% 係数全部8で71.89% (1024にしてもほぼ変わらず)
• (2048, 2048*2, 2048*4, 2048*8) の構成: 75.13% 係数全部8で74.50%

SPARKLEでは、

• (2048*8, 2048*4, 2048*2, 2048): 62.60% 係数次数全部8で60.15% (1024にしてもほぼ変わらず)
• (2048, 2048*2, 2048*4, 2048*8): 63.74% 係数次数全部8で63.54%

荒い方から始めて順に細かくしていった方が明らかに良い。

ソースを切り出して、学習則を具体的に導くことを考える。