やはりTAKの符号が気になる。 再帰的Golomb-Riceに近いだろうというのは読めるが、まだ理解しきれてない。
ffmpegのソースにある、 TAKの残差デコード実装 は以下。コメントを付す:
static const struct CParam {
int init; /* xの初期値のビット幅 */
int escape; /* おそらく、再帰的Golomb-Riceの1段目の閾値 */
int scale; /* おそらく、Golomb-Riceの商部に乗じる係数 */
int aescape; /* おそらく、再帰的Golomb-Riceの2段目の閾値 */
int bias;
} xcodes[50] = { /* aiki: 略 */ };
/* aiki: 略 */
static int decode_segment(TAKDecContext *s, int8_t mode, int32_t *decoded, int len)
{
struct CParam code;
GetBitContext *gb = &s->gb;
int i;
if (!mode) {
memset(decoded, 0, len * sizeof(*decoded));
return 0;
}
if (mode > FF_ARRAY_ELEMS(xcodes))
return AVERROR_INVALIDDATA;
code = xcodes[mode - 1];
for (i = 0; i < len; i++) {
/* aiki: xが最終結果 */
/* aiki: まずcode.initビット読み取った結果をセット(Golomb-Riceの剰余部を先に取得している?) */
unsigned x = get_bits_long(gb, code.init);
if (x >= code.escape && get_bits1(gb)) {
/* aiki: xがcode.escape以上で、続く1ビットが1ならば... (再帰的Golomb-Riceの1段目?) */
/* aiki: 最上位ビットに1をセット 最初の状態からすると x <- get_bits_long(gb, code.init + 1) となるはず */
/* TODO: get_bits1(gb) == 0だった場合はifを抜けるけど、これは何を意味する? */
x |= 1 << code.init;
if (x >= code.aescape) {
/* aiki: xがcode.aescape以上ならば... (再帰的Golomb-Riceの2段目?) */
/* aiki: 商部scaleの取得に入る。まずはα符号の取得。9で止める */
unsigned scale = get_unary(gb, 1, 9);
if (scale == 9) {
/* aiki: scaleが最大の9だったら、scaleの表現ビット数を3ビットで取得 */
/* aiki: 後でcode.biasを足し込む */
int scale_bits = get_bits(gb, 3);
if (scale_bits > 0) {
if (scale_bits == 7) {
/* aiki: scaleの表現ビットが最大の7の場合はさらに5ビット追加で取得 */
scale_bits += get_bits(gb, 5);
/* aiki: scaleが29ビットを超えることはない */
if (scale_bits > 29)
return AVERROR_INVALIDDATA;
}
/* aiki: scaleの差し替え。1だけゲタが入っている */
scale = get_bits_long(gb, scale_bits) + 1;
/* aiki: 商部の加算 */
x += code.scale * scale;
}
/* aiki: code.biasの加算 */
x += code.bias;
} else
/* aiki: 商部の加算。scale < 9の場合はcode.escapeを減じる(TODO: なぜ引くのか?) */
x += code.scale * scale - code.escape;
} else
/* aiki: x > code.aescapeの場合はcode.escapeを減じる */
x -= code.escape;
}
/* aiki: 符号なし整数から符号付き整数に変換 */
decoded[i] = (x >> 1) ^ -(x & 1);
}
return 0;
}
謎のテーブルxcodeの値をプロットしたのが以下:
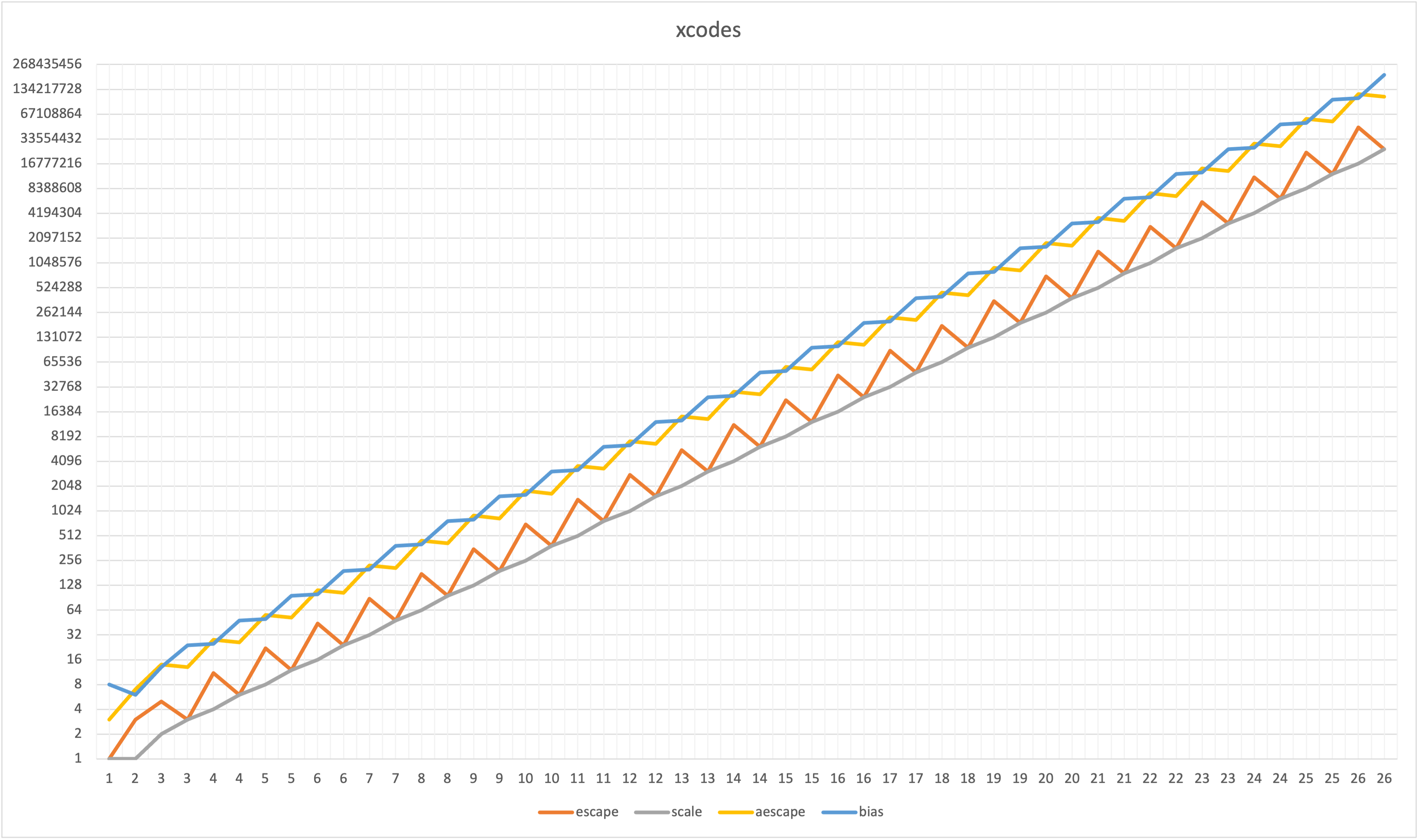
明らかに指数的なトレンドがある。コードの内容を10進数に直すと以下:
| index | init | escape | scale | aescape | bias |
|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 3 | 8 |
| 1 | 2 | 3 | 1 | 7 | 6 |
| 2 | 3 | 5 | 2 | 14 | 13 |
| 3 | 3 | 3 | 3 | 13 | 24 |
| 4 | 4 | 11 | 4 | 28 | 25 |
| 5 | 4 | 6 | 6 | 26 | 48 |
| 6 | 5 | 22 | 8 | 56 | 50 |
| 7 | 5 | 12 | 12 | 52 | 96 |
| 8 | 6 | 44 | 16 | 112 | 100 |
| 9 | 6 | 24 | 24 | 104 | 192 |
| 10 | 7 | 88 | 32 | 224 | 200 |
| 11 | 7 | 48 | 48 | 208 | 384 |
| 12 | 8 | 176 | 64 | 448 | 400 |
| 13 | 8 | 96 | 96 | 416 | 768 |
| 14 | 9 | 352 | 128 | 896 | 800 |
| 15 | 9 | 192 | 192 | 832 | 1536 |
| 16 | 10 | 704 | 256 | 1792 | 1600 |
| 17 | 10 | 384 | 384 | 1664 | 3072 |
| 18 | 11 | 1408 | 512 | 3584 | 3200 |
| 19 | 11 | 768 | 768 | 3328 | 6144 |
| 20 | 12 | 2816 | 1024 | 7168 | 6400 |
| 21 | 12 | 1536 | 1536 | 6656 | 12288 |
| 22 | 13 | 5632 | 2048 | 14336 | 12800 |
| 23 | 13 | 3072 | 3072 | 13312 | 24576 |
| 24 | 14 | 11264 | 4096 | 28672 | 25600 |
| 25 | 14 | 6144 | 6144 | 26624 | 49152 |
| 26 | 15 | 22528 | 8192 | 57344 | 51200 |
| 27 | 15 | 12288 | 12288 | 53248 | 98304 |
| 28 | 16 | 45056 | 16384 | 114688 | 102400 |
| 29 | 16 | 24576 | 24576 | 106496 | 196608 |
| 30 | 17 | 90112 | 32768 | 229376 | 204800 |
| 31 | 17 | 49152 | 49152 | 212992 | 393216 |
| 32 | 18 | 180224 | 65536 | 458752 | 409600 |
| 33 | 18 | 98304 | 98304 | 425984 | 786432 |
| 34 | 19 | 360448 | 131072 | 917504 | 819200 |
| 35 | 19 | 196608 | 196608 | 851968 | 1572864 |
| 36 | 20 | 720896 | 262144 | 1835008 | 1638400 |
| 37 | 20 | 393216 | 393216 | 1703936 | 3145728 |
| 38 | 21 | 1441792 | 524288 | 3670016 | 3276800 |
| 39 | 21 | 786432 | 786432 | 3407872 | 6291456 |
| 40 | 22 | 2883584 | 1048576 | 7340032 | 6553600 |
| 41 | 22 | 1572864 | 1572864 | 6815744 | 12582912 |
| 42 | 23 | 5767168 | 2097152 | 14680064 | 13107200 |
| 43 | 23 | 3145728 | 3145728 | 13631488 | 25165824 |
| 44 | 24 | 11534336 | 4194304 | 29360128 | 26214400 |
| 45 | 24 | 6291456 | 6291456 | 27262976 | 50331648 |
| 46 | 25 | 23068672 | 8388608 | 58720256 | 52428800 |
| 47 | 25 | 12582912 | 12582912 | 54525952 | 100663296 |
| 48 | 26 | 46137344 | 16777216 | 117440512 | 104857600 |
| 49 | 26 | 25165824 | 25165824 | 109051904 | 201326592 |
法則としては、
- 偶数
indexescape:init >= 4でescape = 11 * 2^(init - 4)scale:init >= 2でescape = 2^(init - 2)aescape:init >= 2でaescape = 7 * scalebias:init >= 4でbias = 25 * 2^(init - 4)
- 奇数
indexescape:init >= 3でescape = 6 * 2^(init - 3)scale:init >= 3でscale = 2^(init - 3) + 2^(init - 2)(偶数の間を線形補間)aescape:init >= 3でaescape = scale + 10 * 2^(init - 2)bias:init >= 3でbias = 8 * scale
init <= 2 の領域では法則がほぼ当てはまらないが、この領域は非常に振幅が小さいので指数分布になっておらず、おそらく手探りで決めたのだろう。それ以外での法則は見えたが、背景の理論が見えてこない。
実質、 init がRice符号、 scale がGolomb符号のパラメータになっている。Rice符号だと2のべき乗だけになり、奇数 index の要素は消えることになるが、ここでは補間してよりGolomb符号に近い挙動にしている?
- コードを見ると、初手
init分のビットを取得しているのが目につく。これは剰余部を先に取得している。- 剰余部はRice符号に近い形で実装している。または、再帰的Golomb-Rice符号の1段目を同時にやっている?
- 剰余部は線形量子化するが、商部はこだわっているように思える。α符号は最大9で止めて、それより長ければビット幅+データで表現。