符号で他に思ったことは、Golomb符号の中でも商部が指数分布(ラプラス分布)に従っているはずで、それをハフマン符号化するとよいのではと考えている。 商部はα符号を使っているが、それはp=1/2の幾何分布を仮定しているはず
- 分布を[0,m]で積分すればわかる
- \(\int_{0}^{m} p(x) dx = \int_{0}^{m} \frac{\log(2)}{2m} \exp \left( - \frac{\log(2)}{m} |x| \right) dx = \frac{1}{2}\)
- \(\int_{m}^{2m} p(x) dx = \int_{m}^{2m} \frac{\log(2)}{2m} \exp \left( - \frac{\log(2)}{m} |x| \right) dx = \frac{1}{4}\)
- \(\int_{(k-1)m}^{km} p(x) dx = \int_{(k-1)m}^{km} \frac{\log(2)}{2m} \exp \left( - \frac{\log(2)}{m} |x| \right) dx = 2^{-k-1}\) となるのでα符号が理論上最適。
商だけで見ればそんな大きな値は取らないはず(大きすぎるものは可変長符号で)なので、ハフマン符号は有効に働きそうな気がする。
これはまず商部の観察から始めるべきで、さっそく今のLINNEで商の分布をプロットした。
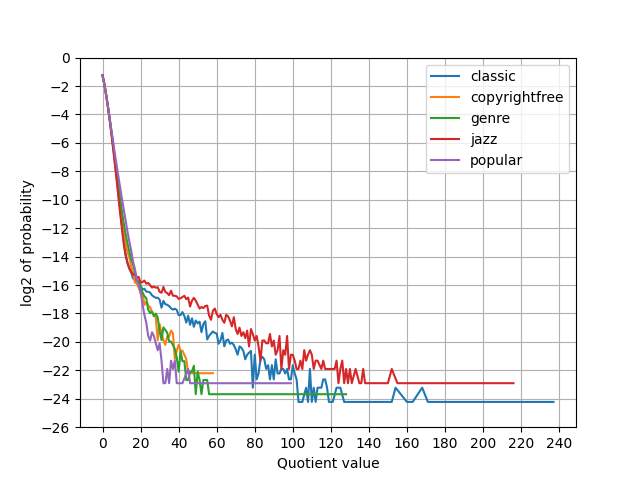
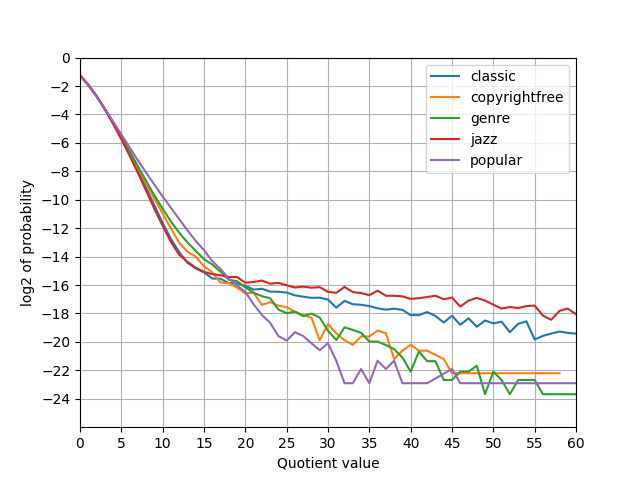
2枚目は横軸を制限しただけでデータは同様。やはり裾が広い。というか、残差を割ってるだけだから残差分布が出てるだけか。 もしα符号で最適ならば、 \(\log_{2}\) の軸上で \(-1-x\) となって直線になるがそうなっていない。 \(x=10\) を超えたあたりで直線とのズレが出る。
商が大きい場合はガンマなりデルタ符号を使うべしということになる。これは以前やってたな。商が大きい場合はガンマ符号に切り替える手法。そして試してみたけど1KB程度の改善に留まっている(SLAでもそんなんだった)。負荷とのトレードオフで考えると美味しくない。
むしろ注目すべきは、商もまた幾何分布に近いというところだろう。早速商をRice符号化したが、悪化。そこまで裾は広くない。
再帰的Golomb-Riceの1段目の符号に偏りがあるのでは?と思ってプロットしたらたしかに大きい数字は出にくい傾向があった。かなり急激に減少する分布であった(エントロピーは7.6)。
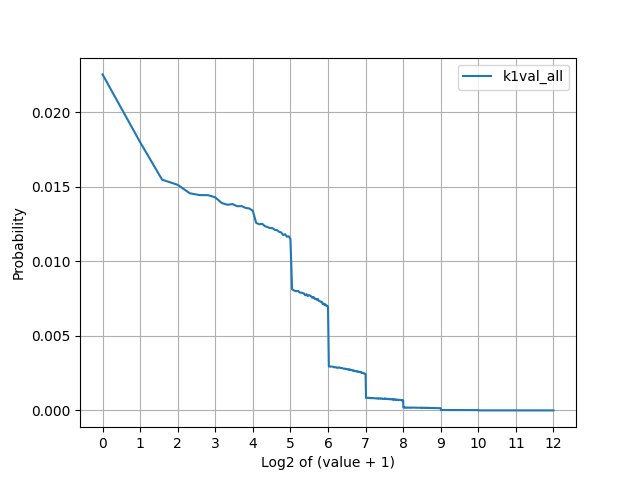
- k1の各パラメータごとの符号分布に注目するとエントロピーがほぼ割当bitと同じで(k1=4のとき3.99...、k1=7のとき6.99...とか)、ほぼ一様分布の様相。偏りは使えなそう。(一方で、ほぼ理想的であると言える)
- その一様分布が重なって上の分布ができている印象(k1が小さいと違うっぽく、一様に近い)。
- 値が小さいとき(2^8=256あたり)はハフマンを使って符号化し、それを超えたらk1を使って2進数出力とか?
- もうちょっと理論詰めたほうがよさそう。実はもう理想的な可能性(現在の符号化で7.6達成済み)を考えている。
- k1の平均をとると6.24と言ってる。これすなわち平均符号長が6.24なので、エントロピーを超えていることになる。
- もうちょっと理論詰めたほうがよさそう。実はもう理想的な可能性(現在の符号化で7.6達成済み)を考えている。
うーん、符号については永遠に終わらん気がしてきたので、フィルタ考察に戻る。その前に、Golomb-Rice符号の長さ解析で、エントロピーと比べたときの冗長度比較を追記しておきたい。
フィルタの考察も進めたい。flakeの観察から、次数をいじるべきではないかと感じてきている。必ずしもパラメータを全て使って予測するべきではないかもしれない(周波数領域でも激しく振動しており、過適合に見える)。分割をしないケースで考えれば良さそう。