総パラメータ数を横軸、L1損失やspectral flatness(Wiener entropy)を縦軸に計算して、なぜ多層構成がいいのかを見ている。
- パラメータの割り振りは全ての層で等しくなるようにした。
- 補助関数法とLevinson-Durbin法でグラフの概形はほぼ変わらなかった。(補助関数法、とても遅い)
- 音源は聖者の行進先頭4秒Lch, アルファベット読み上げLch, 0hz-2500Hzを2秒かけて線形に変化させるチャープ。
結果の図は以下(結果は補助関数法によるものだが、L-Dでもほぼ変わらず):
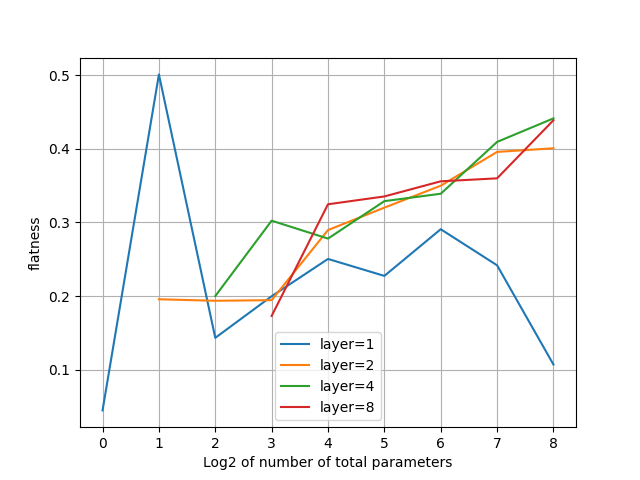
L1ロス
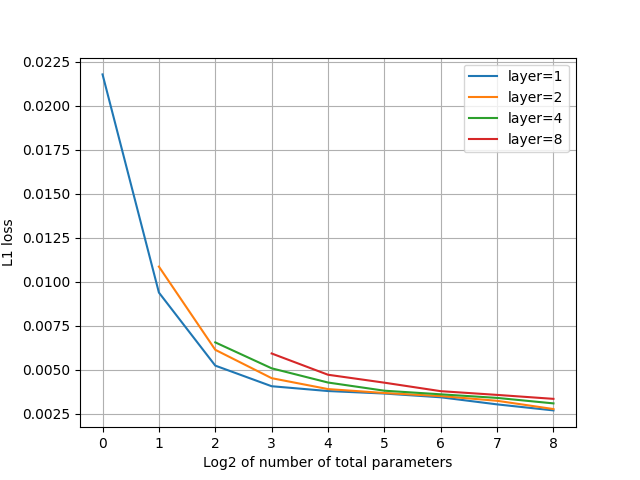
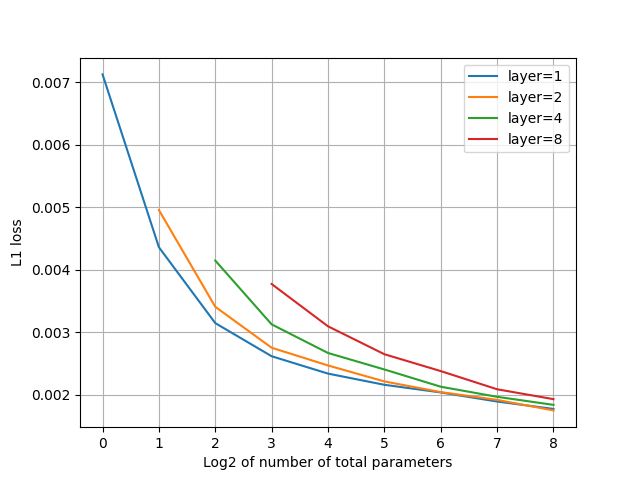
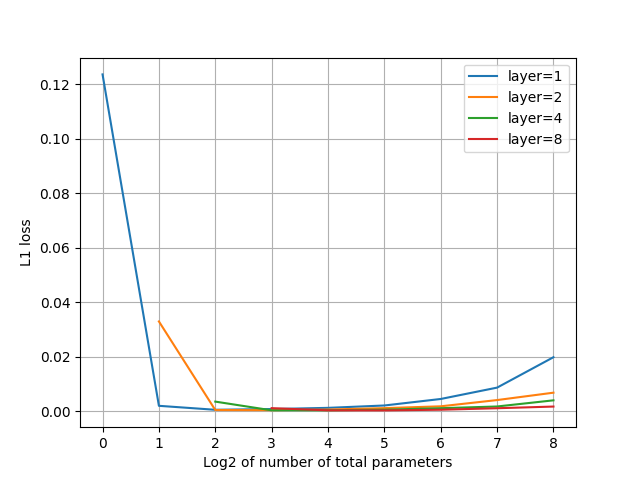
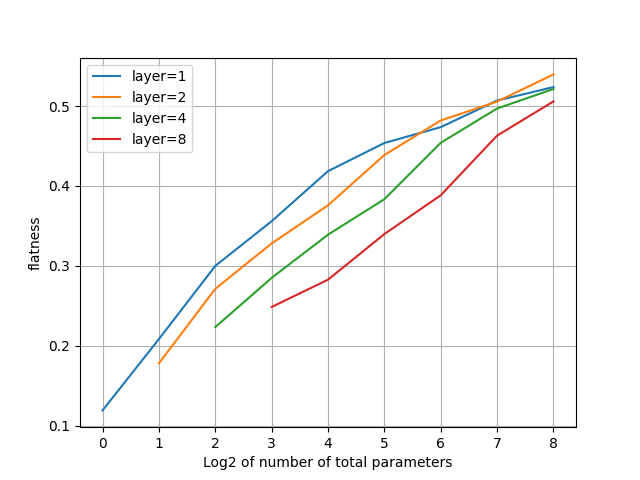
spectral flatness
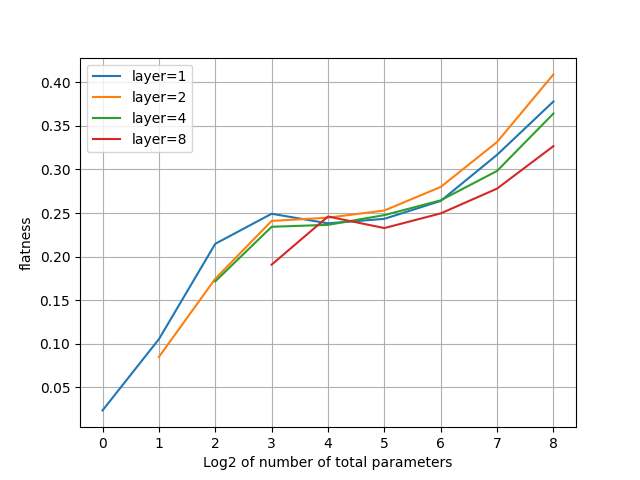
考察
- ロスは1層構成が一番よいが、ほぼ2層構成と同等。パラメータ数を増やすと漸近していく。
- Spectral flatnessはパラメータ数を増やすと2,4,8層構成が良くなる。
Spectral flatnessってそもそも何よ、というところ。今回の場合は、残差がどれくらい白色雑音に近いかを測る尺度以上のことは出てこない・・・
- A spectral-flatness measure for studying the autocorrelation method of linear prediction of speech analysis
- flatnessを使ったLPCの自己相関法等価とのからみ。flatnessの原典ぽいな。
- 自己相関行列の条件数との絡みも書いてある。
- pre-whiteing(プリエンファシス)をすることで大幅に悪条件を防げると言っている。
- こちら でも読める。こっちは要約版。
- Spectral flatness or Wiener Entropy for AR(1) and AR(2)
- AR(1), AR(2)は理論的に計算できる。一般のAR(p)も書いてある。
- Generalization of Spectral Flatness Measure for Non-Gaussian Linear Processes 一般の計算についての原典はここ
- ラプラス分布残差を仮定した場合も計算できるな、おっ…
A spectral-flatness measure for studying ...の論文で条件数が改善するという記述を見て、適応フィルタを入れるのがよさそうと思って、Sign-Sign Algotrithm(SSFilter)を突っ込んだら軒並み改善の傾向。しかし、負荷上昇も間違いないのでオプションにするべきかも。
- RWCで実験してみたら、圧縮率は微悪化かつデコード速度は0.3から0.38くらいまで悪化。
- 負荷に対するゲインがないのでやめる。
Hacker newsで上がっていたwikipediaのLoudness warの記事が面白い。売れた楽曲の音圧は単調に上がっている。一方で歪みまくっている。 参考文献もパット見面白いこと書いてあるので時間があれば腰を入れて読みたい。