リフティングの組み込み検証(8)

LPCへの移行中。昨夜の不具合は残差をもとに予測していたのが問題。in-placeで実行できると勘違いしていた。 そしてなんとなく動くようになったが現在0.1%程度の悪化を観測している。量子化でだいぶ手を抜いているのでそれが原因か。

  • まず、前に経験したようにフィルタ加算前に0.5を加算→だいぶ良くなった。これでほぼPARCORと同等。
  • 前（SLA開発時代）も見たけど量子化ビット幅はあんまりいらないことが分かっている。12bitにした。

結果、ほぼ同一の圧縮性能:

  • MS変換 + 最適プリエンファシス x2 + LPC(4), サブブロックでLPC(4) + CDF42を1段 + 低域でSS(4), 高域でSS(4): 55.0%

これでLPCは一旦いいだろう。再度構成を考えていく。

プリエンファシスによる分散の減少について

TODOにあったプリエンファシスによる分散の減少について考えた。いま、2連結でやってて経験的によくなることが分かっているが、さてどれくらい良いのか。 信号の分散を \(\sigma^{2}\) 、1次,2次の正規化相関をそれぞれ \(\rho_{1}, \rho_{2}\) と書く。平均0の離散時間系列信号 \(x_{n}\) に対して、 \(x_{n} - \rho_{1} x_{n-1}\) の分散は

\begin{align*} E[(x_{n} - \rho_{1} x_{n-1})^{2}] &= E[x_{n}^{2} - \rho_{1} x_{n} x_{n-1} + \rho_{1}^{2} x_{n-1}^{2}] \\ &= E[x_{n}^{2}] - \rho_{1} E[x_{n} x_{n-1}] + \rho_{1}^{2} E[x_{n-1}^{2}] \\ &= \sigma^{2} - 2 \rho_{1}^{2} \sigma^{2} + \rho_{1}^{2} \sigma^{2} \\ &= \sigma^{2} (1 - \rho_{1}^{2}) \end{align*}

となる。（これは1次のLPCなので、最小の分散を達成している。）さて、この操作の後になおも残る1次の相関は、

\begin{align*} E[(x_{n} - \rho_{1} x_{n-1})(x_{n-1} - \rho_{1}x_{n-2})] &= E[x_{n}x_{n-1} - \rho_{1} x_{n} x_{n-2} - \rho_{1} x_{n-1}^{2} + \rho_{1}^{2} x_{n-1} x_{n-2}] \\ &= \rho_{1} \sigma^{2} - \rho_{1} \rho_{2} \sigma^{2} - \rho_{1} \sigma^{2} + \rho_{1}^{3} \sigma^{2} \\ &= \sigma^{2} \rho_{1} (\rho_{1}^{2} - \rho_{2}) \end{align*}

より、分散で割って正規化すると \(\frac{\rho_{1} (\rho_{1}^{2} - \rho_{2})}{1 - \rho_{1}^{2}}\) となる。この正規化相関を使ってもう一度プリエンファシスをかけると、分散は

\begin{equation*} E[(x_{n} - \rho_{1} x_{n-1})^{2}] \left[ 1 - \left\{ \frac{\rho_{1} (\rho_{1}^{2} - \rho_{2})}{1 - \rho_{1}^{2}} \right\}^{2} \right] = \sigma^{2} (1 - \rho_{1}^{2}) \left[ 1 - \left\{ \frac{\rho_{1} (\rho_{1}^{2} - \rho_{2})}{1 - \rho_{1}^{2}} \right\}^{2} \right] \end{equation*}

となって、元の分散 \(\sigma^{2}\) と比を取ると

\begin{equation*} (1 - \rho_{1}^{2}) \left[ 1 - \left\{ \frac{\rho_{1} (\rho_{1}^{2} - \rho_{2})}{1 - \rho_{1}^{2}} \right\}^{2} \right] \end{equation*}

だけ分散が減少することになる。どんな感じになるかプロットしたのが以下：

分散比

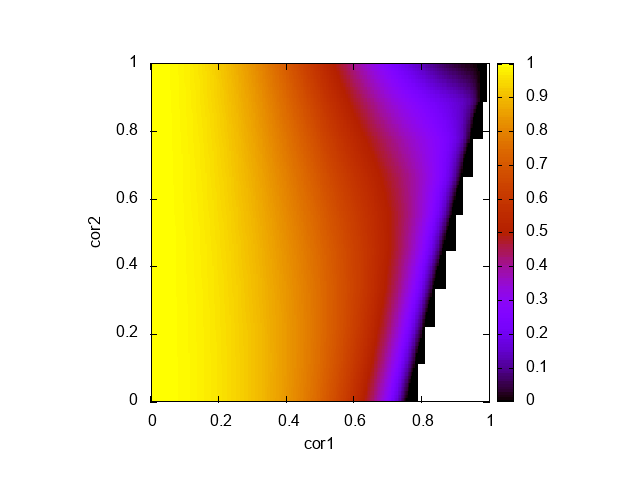
色がついていない領域は負値を取っている（実現できない値？） 大体の音声では \(\rho_{1} \approx 0.9\) を取るので（低域成分がオーバーサンプリングされているから）、 \(\rho_{2}\) に関係なく相当の分散減少が期待できる。

プリエンファシスを1回だけ行った場合の分散比 \((1 - \rho_{1}^{2})\) と比べ、 \(\left\{ \frac{\rho_{1} (\rho_{1}^{2} - \rho_{2})}{1 - \rho_{1}^{2}} \right\}^{2} \geq 0\) だからより小さくなるはずである。

時間をおいて銭湯サウナでぼんやりしてたら、上記って必ずしも最適では無い気がしてきた。要は、2パラメータ \(a,b\) があって、 \(y_{n} = x_{n} - a x_{n-1}, z_{n} = y_{n} - b y_{n-1}\) としたとき、分散 \(E[z_{n}^{2}]\) を最小にする \(a,b\) は少なくとも \(a=\rho_{1}\) とは限らない気がしている。もっと小さい値を取れるはずじゃないのか。

多分、もっと良いパラメータ組 \((a,b)\) があると踏んでいる。なぜならプリエンファシスは直交変換ではないように見えるから。1次の相関が残っているところを見ると、分散をより小さくする変換があるはず。早速試してるけど簡単に見た感じでは難しそう。小さくできれば利益が大きい。1日考えてみようか。

と思ったが、冷静になる（ならなくても）と、

\begin{equation*} z_{n} = (x_{n} - a x_{n-1}) - b (x_{n-1} - a x_{n-2}) = x_{n} - (a + b) x_{n-1} + ab x_{n-2} \end{equation*}

となってその分散の最小化を考えているので、結局プリエンファシス2段で最適なのは2次のプリエンファシスということになる。しかし、1次を2段重ねることとの差をちゃんと見たい。