リフティングの組み込み検証(9)

早速2段階プリエンファシスを2次のLPCに切り替えてみた。予想としては丸め誤差除き同じになると思っていたが、

  • MS変換 + LPC(2) + LPC(4), サブブロックでLPC(4) + CDF42を1段 + 低域でSS(4), 高域でSS(4): 55.3%

0.3%悪化。これは有意に差があるといえるだろう。数値演算誤差だけの話じゃないと思う。 そしてLPC(2)使用時の分散と2段プリエンファシスの分散を比較しようと思った。これも同じと思っていたが、、、違う…

LPC(2)のときの分散は、

\begin{align*} E[z_{2}^{2}] &= E[\left\{ x_{n} - a_{1} x_{n-1} - a_{2} x_{n-2} \right\}^{2}] \\ &= \sigma^{2} (1 + a_{1}^{2} + a_{2}^{2} - 2 \rho_{1} a_{1} - 2 \rho_{2} a_{2} + 2 \rho_{1} a_{1} a_{2}) \end{align*}

より、これを係数で偏微分すると

\begin{align*} \frac{\partial}{\partial a_{1}} E[z_{2}^{2}] &= 2\sigma^{2} (c - \rho_{1} + \rho_{1}d) \\ \frac{\partial}{\partial a_{2}} E[z_{2}^{2}] &= 2\sigma^{2} (d - \rho_{2} + \rho_{1}c) \end{align*}

で、それぞれ0とおいて \(a_{1}, a_{2}\) について解くと（省略）

\begin{equation*} a_{1} = \frac{\rho_{1}(1 - \rho_{2})}{1 - \rho_{1}^{2}}, a_{2} = \frac{\rho_{2} - \rho_{1}^{2}}{1 - \rho_{1}^{2}} \end{equation*}

これを \(E[z_{2}^{2}]\) に代入してプロットすると以下のようになる（きれいな式に整理できなかったので苦し紛れにプロット）

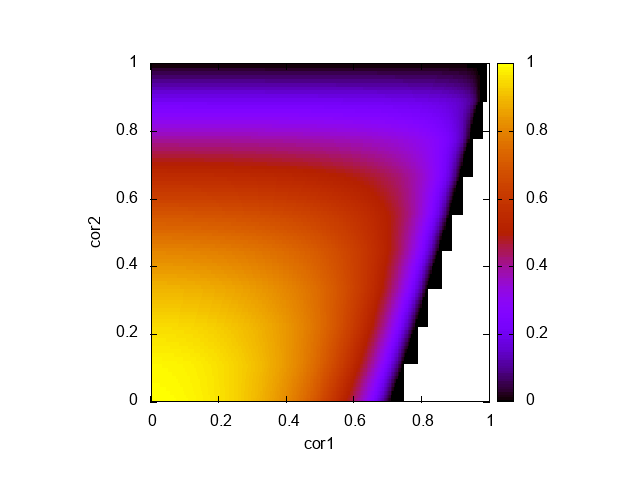
LPC(2)分散比

明らかに2段プリエンファシスとは違う。 \(\rho_{2} \approx 1\) でも分散が小さくなる。そして、2段プリエンファシスとの比較として、 \(\text{(2段プリエンファシスの分散比)} - \text{(LPC(2)の分散比)}\) をプロットした結果が以下。

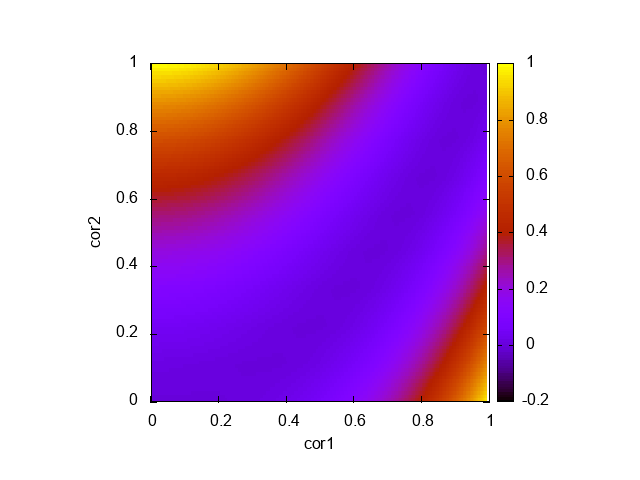
分散比の比較

殆どの領域でLPC(2)の方が分散をよく減らしていることがわかる。kanonop.wavでも、LPC(2)のトータル分散は0.001947, プリエンファシス2段は0.002008だったので実際に分散削減効果はLPC(2)の方が高い。

では、2段プリエンファシスの方がより良い圧縮性能に寄与していたのはなぜ？

kanonop.wavのトータル正規化相関を見ると、LPC(2)は0.383299、プリエンファシス2段は0.377010で、プリエンファシス2段の方が1次の相関を消せている事がわかる。この結果のみから考えると、1次相関を減らすことが大事ということか？いや、まだ時期尚早。2次相関まで見ておく。LPC(2)は-0.421879、プリエンファシス2段は-0.454856だった。2次相関はLPC(2)の方が絶対値が小さい。

すると、1次相関を消すのが大事ということ？最適なフィルタ設計もできるで試してみる。 フィルタ係数を \(a\) とする。1フィルタ処理後の1次相関は、

\begin{align*} E[(x_{n} - ax_{n-1})(x_{n-1} - ax_{n-2})] &= E[x_{n}x_{n-1} - ax_{n}x_{n-2} - ax_{n-1}^{2} + a^{2}x_{n-1}x_{n-2}] \\ &= \sigma^{2} (\rho_{1} - \rho_{2} a - a + \rho_{1} a^{2}) \\ &= \sigma^{2} \left\{ \rho_{1} \left( a^{2} - \frac{1 + \rho_{2}}{\rho_{1}} a \right) + \rho_{1} \right\} \\ &= \sigma^{2} \left\{ \rho_{1} \left( a - \frac{1 + \rho_{2}}{2\rho_{1}} \right)^{2} + \rho_{1} - \frac{(1 + \rho_{2})^{2}}{4\rho_{1}} \right\} \end{align*}

だから \(a\) に関して凸な関数になっている。実信号では \(\rho_{1} > 0\) だから下に凸と考えていい。そして、

\begin{equation*} a = \frac{1 + \rho_{2}}{2\rho_{1}} \end{equation*}

とすれば最小値 \(\rho_{1} - \frac{(1 + \rho_{2})^{2}}{4\rho_{1}}\) が達成できる。この係数を使って2回適用してみた。すると、1次相関が 0.324132 になって54.9%を叩き出した。分散は0.002333で悪いのだが最終的な圧縮率はよい。これは効いているし、 1次相関を消すことが重要であることを示している 。そして今は1次のフィルタだったけど、n次でも良いわけだから試してみたい。

一方、1次相関が0になるときの \(a\) は、

\begin{equation*} a = \frac{1 + \rho_{2}}{2\rho_{1}} \pm \sqrt{ \left(\frac{1 + \rho_{2}}{2\rho_{1}} \right)^{2} - 1} \end{equation*}

となるが、実装したところ発散した。おそらく上記方程式の判別式が負で解無し（ルートの中身が負に）になっている？判別式 \(\left(\frac{1 + \rho_{2}}{\rho_{1}} \right)^{2} - 4\) が正、すなわち

\begin{align*} \left(\frac{1 + \rho_{2}}{\rho_{1}} \right)^{2} - 4 > 0 &\iff \left| \frac{1 + \rho_{2}}{\rho_{1}} \right| > 2 \\ &\iff \left| \frac{1 + \rho_{2}}{2\rho_{1}} \right| > 1 \end{align*}

ならば解を使うのが良いという示唆かもしれない。2段で早速使ってみたら、分散0.002227、1次相関0.325073、2次相関-0.546465で圧縮率は54.9%だけど解を直接使うより良くなってる。

2次以上については要調査。